Se una funzione $f(x)$ è positiva e integrabile, cioè $\int_0^\infty f(x)$ è un numero finito, allora è vero che $f(x) \to 0$ per $x \to \infty$? Come vedremo fra poco, la risposta è no. Tuttavia questa proprietà viene spesso presa per vera, ad esempio nella soluzione dell’equazione di Schrodinger. In questo articolo vediamo quali sono le condizioni esatte perché ciò si verifichi. In quanto segue $f(x)$ è positiva e integrabile.
Una funzione integrabile senza limite all’infinito
Abbiamo detto che anche se $f(x)$ è positiva e integrabile, non è detto che tenda a zero all’infinito. È però chiaro che se se $f(x)$ tende ad un numero diverso da zero all’infinito, allora il suo integrale sarà divergente. Infatti se $f(x) \to c$ per $x \to \infty$ allora fissando un $\epsilon > 0$, $\exists\,\, M \,\,\mathrm{t.c.}\,\, c-\epsilon<f(x)<c+\epsilon\,\,\forall\,\,x>M$. Poiché $f(x)>0$ e $c\neq 0$ allora $c>0$. Quindi prendiamo $\epsilon=c/2$, in modo che $f(x)>c/2$. Quindi
$$\int_{0}^{\infty} f(x) dx \geq \int_{M}^{\infty} f(x) dx >\int_{M}^{\infty} \frac{c}{2} dx = \infty$$
D’altro canto all’infinito $f$ può avere quattro comportamenti diversi: può divergere, può convergere a un numero positivo, può convergere a $0$, può non avere limite. Pertanto se $f$ è integrabile e non converge a $0$, non può avere limite all’infinito.
Ora costruiamo una funzione positiva e integrabile ma senza limite all’infinito. Inoltre la funzione sarà anche illimitata, per cui non è neanche vero che se $f(x)$ è integrabile allora è limitata. La funzione è ha il grafico seguente:
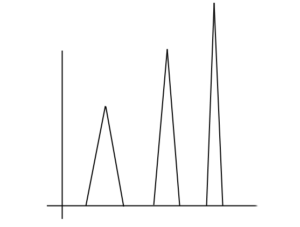
Versione stilizzata della funzione integrabile ma illimitata.
In altre parole, in ogni numero intero mettiamo un triangolo con altezza $n$ e base $1/n^3$. Altrove la funzione è esattamente zero. L’area di una picca è quindi $1/2n^2$ e quindi l’integrale vale
$$\int_0^{\infty} f(x) dx = \sum_{n=1}^\infty \frac{1}{2n^2} = \frac{\pi^2}{12}$$
Pertanto una funzione integrabile non deve necessariamente essere limitata, né deve necessariamente tendere a 0.
Un raffinamento all’esempio precedente
La funzione dell’esempio precedente non è continua, tuttavia la continuità non cambia il risultato finale. Possiamo cioè costruire una funzione continua, integrabile, illimitata e senza limite all’infinito. Per farlo utilizziamo la funzione a supporto compatto di cui abbiamo parlato negli articoli precedenti. Ovvero sostituiamo ogni triangolo con una montagnetta che parte da $0$, arriva ad $n$, dove forma un piccolo plateau, e poi ritorna in $0$. La descrizione matematica è complicata, ma l’idea è chiara. Inoltre una funzione del genere è infinitamente derivabile, per cui neanche la derivabilità basta a garantire che $f(x) \to 0$ all’infinito o che $f(x)$ sia limitata.
Una funzione integrabile la cui derivata non ha limite
Abbiamo quindi mostrato che esiste una funzione $f$ infinitamente derivabile e integrabile, che è però illimitata e non ha limite all’infinito. In meccanica quantistica tuttavia la situazione è leggermente diversa. Abbiamo infatti la funzione d’onda $\psi(x)$ che è quadrato-integrabile, e di solito imponiamo una condizione sulla sua derivata $\psi'(x)$.
Tuttavia se anche $\psi(x)$ è quadrato-integrabile, come abbiamo visto ciò di certo non implica che $\psi(x) \to 0$, ma non implica neanche che $\psi'(x)\to 0$. Infatti seguendo questo post possiamo considerare la funzione:
$$\psi(x) = \frac{\sin{x^2}}{\sqrt{x^2+1}}$$
In questo caso $\psi(x)^2$ è integrabile perché è positiva e dappertutto minore o uguale a $1/(x^2+1)$, che è integrabile. Tuttavia la sua derivata tende a $2\cos{x^2}$, per cui non ha limite all’infinito.
Alcune condizioni sufficienti
Dopo tutte queste condizioni negative, diamo una condizione positiva. Cioè diamo finalmente delle condizioni per cui il limite tenda a $0$.
Proposizione. Se $\psi$ e $\psi’$ sono quadrato-integrabili, allora $\psi \to 0$ per $x \to \infty$ e $\psi$ è limitata.
La dimostrazione la trovate qui. Ciò non implica nulla tuttavia sul limite di $\psi’$. Ad ogni modo il requisito che $\psi’$ sia quadrato integrabile non risponde ad alcun significato fisico, ed è quindi del tutto arbitrario. Alla stessa maniera,
Proposizione. Se $f$ e $f’$ sono assolutamente integrabili, allora $f \to 0$ per $x \to \infty$.
Abbiamo anche la seguente condizione, che vale in genere per funzioni continue, senza nessuna condizione di integrabilità:
Proposizione. Se $f$ e $f’$ sono funzioni continue e il limite per $x \to \infty$ esiste per entrambe, allora $\lim_{x \to \infty} f’ = 0$.
Una dimostrazione particolarmente bella di questo fatto è nella seconda risposta a questa domanda). La condizione che il limite della derivata esista è cruciale, perché come abbiamo visto potrebbe semplicemente non esistere.
In ogni caso abbiamo questo risultato interessante:
Proposizione. Se $f$ è integrabile, allora $\lim_{n\to \infty} f(n x)=0$ per quasi ogni $x$.
Questa condizione significa che, con l’eccezione di un insieme di misura nulla, partendo da $x$ e saltando a intervalli interi, prima o poi la funzione tenderà a zero. Intuitivamente ciò significa che la funzione a lungo andare avrà delle grosse isole in cui sarà arbitrariamente vicina allo zero, e solo in alcuni punti ciò non accadrà. Nell’esempio della funzione “picca” che abbiamo dato prima, gli unici punti che non tenderanno a zero all’infinito sono le punte delle picche.
Per finire, diamo la condizione più importante, cioè quella che permette di dedurre che il limite sia zero a partire dall’integrabilità:
Proposizione. Sia $f$ integrabile e uniformemente continua su $\mathbb{R}$. Allora il suo limite all’infinito è zero.
La dimostrazione la trovate qui. Tuttavia la continuità uniforme è una condizione molto forte, più forte sia della derivabilità che della continuità della derivata. È vero che una funzione continua e limitata in un insieme compatto è uniformemente continua, ma a noi interessa proprio il caso dell’infinito, cioè un insieme non compatto. La continuità uniform è problematica anche perché non ammette una chiara interpretazione fisica, per cui non è chiaro perché dovrebbe essere soddisfatta dalla funzione d’onda.
La morale della favola
Alla fin fine talvolta alcuni requisiti che imponiamo in fisica non sono esattamente giustificabili dal punto matematico, eppure comunque corretti da un punto di vista fisico. Nel caso della meccanica quantistica, l’imposizione che $\psi, \psi’ \to 0$ all’$\infty$ è giustificato dal principio generale di località, secondo cui è possibile ignorare tutto ciò che avviene sufficientemente lontano da un certo esperimento.
