Abbiamo due dielettrici con indice di rifrazione $n$ separati da una regione di vuoto larga $d$, come in figura:
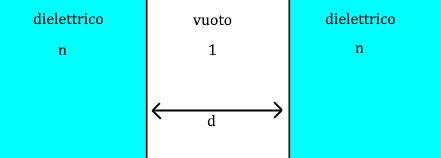
Un’onda è incidente da sinistra con angolo $\theta_I$ tale che $n \sin{\theta_I}>1$ così che ci sia riflessione totale. Nel vuoto si propagano due onde evanescenti con vettore di fase complesso, una che cresce esponenzialmente e una che decade esponenzialmente.
Senza il secondo dielettrico l’onda crescente non sarebbe fisicamente possibile e avremmo solo il fenomeno della riflessione interna totale. Se invece abbiamo il secondo dielettrico, entrambe le onde sono possibili e hanno effetto sull’onda trasmessa nel secondo dielettrico. In tal caso la riflessione è detta “frustrata”.
Quello che ci interessa calcolare è la frazione di energia trasmessa, data da
$$\left| \frac{E_T}{E_I} \right|^2 $$
dove $E_T$ è il coefficiente del campo elettrico trasmesso, e $E_I$ è il coefficiente del campo elettrico incidente. Tale calcolo è difficile, ma è fattibile tenendo implicito tutto ciò che non serve per i conti.
Chiamiamo le tre regioni $1$, $2$ e $3$. Teniamo implicita la dipendenza dal tempo, e per semplicità poniamo $E_I = 1$. Allora i campi elettrici nelle tre regioni sono:
$\begin{cases} E_1 = e^{-i k_I x} + R e^{i k_I x} \\ E_2 = A e^{-\beta x} + B e^{\beta x} \\ E_3 = T e^{-i k_I x} \end{cases}$
e i corrispondenti campi magnetici:
$\begin{cases} B_1 = \frac{k_I}{\omega} (e^{-i k_I x} – R e^{i k_I x}) \\ B_2 = \frac{i \beta}{\omega} (A e^{-\beta x} – B e^{\beta x}) \\ B_3 =\frac{k_I}{\omega} T e^{-i k_I x} \end{cases}$
Per semplicità abbiamo definito $k_I = k \cos{\theta_I}$ e $\beta = k \sqrt{\sin^2{\theta_I}-1/n^2}$, relazione che abbiamo ottenuto dalla legge di Snell.
Imponendo la continuità dei campi per $x=0$ (prima interfaccia) e $x=d$ (seconda interfaccia) otteniamo quattro equazioni in quattro incognite ($R$, $A$, $B$, $T$):
$\begin{cases} 1+R = A+B \\ A e^{-\beta d} + B e^{\beta d} = T e^{-i k_I d} \\ k_I (1-R) = i\beta (A-B) \\ i\beta (A e^{-\beta d} – B e^{\beta d}) = k_I T e^{-i k_I d} \end{cases}$
Ci interessa solo $T$. Eliminando $R$ e $T$ dalle equazioni otteniamo:
$\begin{cases} k_I (2-A-B) = i\beta (A-B) \\ i\beta (A e^{-\beta d} -B e^{\beta d}) = k_I (A e^{-\beta d} + B e^{\beta d}) \end{cases}$
Risolvendo otteniamo:
$$\begin{cases} A = \frac{2(is +1) e^{\beta d}}{(is +1)^2 e^{\beta d} – (is -1)^2 e^{-\beta d}} \\ B = \frac{2(is -1) e^{-\beta d}}{(is +1)^2 e^{\beta d} – (is -1)^2 e^{-\beta d}} \end{cases}$$
dove per semplicità abbiamo definito $s = \beta/k_I$. Sostituendo nuovamente dentro il sistema otteniamo
$$T=e^{i k_I d} (A e^{-\beta d} + B e^{\beta d}) = e^{i k_I d} \frac{4 i s}{(is +1)^2 e^{\beta d} -(is -1)^2 e^{-\beta d}}$$
Quindi
\begin{align*}
\frac{1}{|T|^2} &= \left| \frac{(is +1)^2 e^{\beta d} -(is -1)^2 e^{-\beta d}}{4 i s} \right|^2 = \\
&=\left| \frac{e^{\beta d}+e^{-\beta d}}{2} -\frac{i (1-s^2)}{2s} \frac{e^{\beta d}-e^{-\beta d}}{2}\right|^2 = 1 + \frac{(1+s^2)^2}{4s^2} \sinh^2{\beta d}
\end{align*}
Chiamiamo $\gamma = \frac{1+s}{2s} = \frac{k (1-1/n^2)}{2\beta \cos{\theta_I}}$. Pertanto otteniamo:
$$\left| \frac{E_T}{E_I} \right|^2 = \frac{1}{1+\gamma^2 \sinh^2{\beta d}}$$
Da questa formula deduciamo che più è larga la zona vuota, minore è la frazione di energia trasmessa. Per l’angolo di riflessione totale ($n \sin{\theta_I} = 1$), tutta l’energia viene trasmessa dall’altra parte del vuoto.
