Il concetto di rottura spontanea di simmetria è parecchio complesso, e se non viene trattato in maniera appropriata può portare a delle contraddizioni. Consideriamo il caso più semplice, il modello di Ising in due dimensioni con Hamiltoniana
$$\mathcal{H} = -J \sum_{\langle x y \rangle} s_x s_y$$
dove $\langle x y \rangle$ sono siti primi vicini. È noto che il modello ha una simmetria $\Z_2$ data da $s_x \to -s_x$. Poniamo $J=1$ per semplicità, dato che qui non è importante. La funzione di partizione è data da
$$Z[\beta, N] = \sum_{\{s\}} \exp{\pqty{-\beta \mathcal{H}(\{s\})}}$$
dove la somma su $\{s\}$ è una somma su tutte le possibili configurazioni di spin. Sappiamo bene che questo modello ha una transizione di fase. La magnetizzazione è data da
$$m(\beta, N) = \frac{1}{N} \expval{\sum_x s_x}$$
dove $N$ è il numero di spin. Per $\beta$ piccolo cioè alte temperature abbiamo una fase disordinata in cui gli spin puntano tutti in direzioni a caso e quindi $m = 0$, mentre per $\beta$ grande, ovvero basse temperature, gli spin punteranno o tutti su o tutti giù e quindi $m \neq 0$. Tuttavia vediamo subito che abbiamo un’apparente contraddizione. Infatti se calcoliamo la magnetizzazione analiticamente abbiamo
$$m(\beta, N) = \frac{1}{N} \expval{\sum_x s_x} =\frac{1}{Z} \sum_{\{s\}} \pqty{\sum_x s_x }\exp{\pqty{-\beta \mathcal{H}(\{s\})}}$$
Ora mandando tutti gli spin $s_x \to -s_x$ l’Hamiltoniana non cambia e la somma su tutti gli spin non cambia, così come la funzione di partizione. Tuttavia $\sum_x s_x \to -\sum_x s_x$ e quindi otteniamo il risultato paradossale $m=-m$, cioè $m=0$. Ovvero sembrerebbe che la magnetizzazione è sempre nulla contrariamente a quanto si dice di solito. Poiché è nulla per ogni $\beta$ e per ogni $N$, è nulla anche nel limite termodinamico $N \to \infty$.
Questo problema è ben noto e anche la sua soluzione. Prima di tutto introduciamo un campo esterno $h$ che rompe la simmetria $\Z_2$. La funzione di partizione è quindi
$$Z[\beta, h, N] = \sum_{\{s\}} \exp{\bqty{-\beta \pqty{\mathcal{H}(\{s\})+h \sum_x s_x}}}$$
Ora se effettuiamo di nuovo il calcolo di $m(\beta, h, N)$ non troveremo più $m=0$ perché riflettendo gli spin $s_x \to -s_x$ la funzione di partizione non rimane più invariante a causa del campo esterno $h$. Per ritrovare la simmetria dovremmo mandare anche $h \to -h$ e in questa maniera otterremmo $m(\beta, h, N)=-m(\beta, -h, N)$, che tuttavia non è quello che ci interessa. Chiaramente nel problema iniziale $h$ non c’è e quindi va rimosso in qualche maniera. Tuttavia calcolando il limite $h \to 0$ torniamo al punto di prima. La soluzione sta nel calcolare prima di tutto il limite termodinamico, e solo poi mandare $h \to 0$. Ovvero definiamo la magnetizzazione $m(\beta)$ tramite il limite seguente:
$$m(\beta) = \lim_{h \to 0} \lim_{N \to \infty} m(\beta, h, N)$$
Si può dimostrare rigorosamente che $m(\beta)$ ha il comportamento corretto: è nulla per $\beta < \beta_c$ (fase disordinata) e non nulla in $\beta > \beta_c$ (fase ordinata). Se avessimo preso i limiti al contrario, ovvero se avessimo prima mandato $h\to 0$ e poi $N\to \infty$ avremmo ritrovato il caso precedente in cui $m(\beta, 0, N)=0$ e quindi $m(\beta)\equiv 0$. In altre parole i due limiti non commutano:
$$ \lim_{h \to 0} \lim_{N \to \infty} \neq \lim_{N \to \infty} \lim_{h \to 0} $$
Ciò mostra che:
- la rottura spontanea di simmetria avviene solo nel limite termodinamico;
- un sistema in cui una simmetria è rotta spontaneamente è molto sensibile anche a perturbazioni arbitrariamente piccole.
D’altronde, pensandoci meglio, non avremmo potuto aspettarci altro: nella fase ordinata gli spin sono tutti allineati e quindi la magnetizzazione sarà $+1$ oppure $-1$. Tuttavia entrambe le possibilità sono equamente probabili e non è chiaro quale numero debba assumere $m$: $+1$ o $-1$? Poiché appunto ciò non è prevedibile a priori, la risposta è la somma di tutte le varie possibilità, e poiché le varie possibilità sono collegate l’una con l’altra da una trasformazione di simmetria, il valore totale è nullo, $m=1-1=0$. L’introduzione di un campo esterno cambia questo discorso, poiché gli spin tenderanno ad allinearsi col campo esterno: se $h$ è positivo allora gli spin saranno tutti $+1$ e quindi naturalmente $m=+1$; invece se $h$ è negativo allora naturalmente $m=-1$. Ciò mostra che per quanto sia minuscolo, $h$ ha un effetto decisivo sulla magnetizzazione del sistema; inoltre il limite $h\to 0$ non è propriamente definito, ma è diverso dai due lati $0^{\pm}$ sebbene (per $\beta > \beta_c$) in entrambi i casi sia non-zero.
Un’altra maniera di vedere la cosa è la seguente. Consideriamo l’energia libera $F(m)$ in funzione della magnetizzazione $m$ ottenuta nel solito metodo nella teoria di Landau:

La parte verde rappresenta l’energia libera nella fase disordinata, in cui c’è un unico minimo in $m=0$. La parte verde invece è l’energia libera nella fase ordinata, in cui abbiamo due minimi in $m= \pm 1$, mentre ora $m=0$ è diventato un massimo. Tanto i minimi quanto i massimi sono punti di equilibrio, ma solo i minimi sono stabili. Ora se noi immaginiamo di trovarci esattamente nel minimo della fase disordinata e di cambiare lentamente la temperatura andando nella fase ordinata, allora rimarremo sempre nel punto di equilibrio $m=0$. Ora però questo è un massimo, non un minimo, e quindi qualsiasi perturbazione casuale, per quanto piccola, destabilizzerà la magnetizzazione e la farà cadere in uno dei due veri minimi. In questo senso l’introduzione del campo esterno $h$ è una necessità per modellare la presenza di forze anche minuscole nella vera situazione fisica ed evitare che il sistema rimanga artificialmente intrappolato in un punto di equilibrio instabile.
Possiamo caratterizzare la necessità di introdurre $h$ anche in un’altra, ultima, maniera. Notiamo che la simmetria $\Z_2$ che rovescia gli spin, $s_x \to -s_x$ è ambigua: possiamo vederla sia come un’operazione fisica, in cui prendiamo ogni singolo spin e lo rovesciamo, sia come un cambiamento di punto di vista, in cui semplicemente invece di guardare gli spin “dall’alto”, li guardiamo “dal basso”, dalla cui prospettiva saranno tutti rovesciati. Mentre nel primo caso la simmetria è una vera trasformazione, e quindi può essere rotta, nel secondo caso la simmetria è semplicemente un cambio di prospettiva, o un cambio di sistema di coordinate (o anche una simmetria di calibro), e perciò non può essere rotta; possiamo sempre, infatti decidere di guardare il sistema dall’alto o dal basso. Il punto è che l’Hamiltoniana iniziale non ci permette di distinguere tra le due, perché in termini pratici sono identiche ed entrambe operano mandando $s_x \to -s_x$. Ciò non è più vero se introduciamo $h$. In tal caso, come abbiamo visto, possiamo distinguere due simmetrie:
- la simmetria per cui $s_x \to -s_x$ e $h \to h$. Questa è la vera simmetria $\Z_2$ in cui prendiamo ogni spin e lo rovesciamo, ma non facciamo niente ad $h$.
- la simmetria per cui $s_x \to -s_x$ e $h \to -h$. Questa è il cambio di prospettiva, sempre una simmetria $\Z_2$ ma che corrisponde semplicemente al guardare il sistema dall’alto o dal basso.
In altre parole $h$ ci fornisce un’orientazione che permette di distinguere le due direzioni su e giù, e ora possiamo quindi distinguere la simmetria vera dalla simmetria artificiale di calibro. Come sappiamo, la simmetria di calibro non può essere rotta per definizione, perché possiamo sempre cambiare la prospettiva, perciò prima di poter rompere la simmetria $\Z_2$ dobbiamo distinguerla dal semplice cambio di prospettiva introducendo $h$.
Un’ultima illustrazione del problema riguarda la possibilità di simularlo numericamente tramite metodi Monte Carlo. Non spiegheremo i dettagli ma in pratica possiamo calcolare un’osservabile, in questo caso la magnetizzazione $m$, mentre il sistema evolve; la risposta finale sarà la media di tutti i valori ottenuti. Due esempi per $N=8$ e $N=16$ nella fase ordinata sono mostrati in figura:
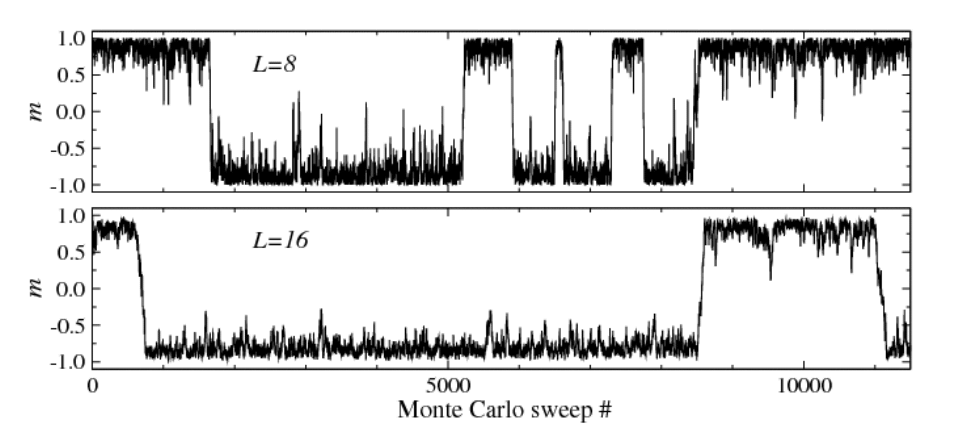
In questo caso non c’è nessun campo esterno. Vediamo che in entrambi i casi il sistema si trova per lunghi periodi o in un punto in cui $m=1$ o in un punto in cui $m=-1$. Tuttavia poiché appunto non gli stiamo dando un’indicazione esterna, il sistema è libero di oscillare tra le due. Se facessimo andare il sistema a lungo e poi calcolassimo la media, otterremmo in totale $m \approx 0$ come è abbastanza chiaro nella prima immagine. La differenza tra la prima e la seconda immagine è che per $N=16$ abbiamo molti meno eventi di transizione tra $+1$ e $-1$, e il sistema è bloccato in uno o l’altro minimo. Ciò è parallelo a quanto facevamo prima: in questo caso la perturbazione casuale è dovuta alla scelta casuale di un’inizializzazione del sistema, e al fatto che esso stesso evolve in maniera stocastica perché così funziona l’algoritmo. Tuttavia appunto per $N$ finito il sistema può ancora spostarsi da un minimo all’altro, ed è solo nel limite $N \to \infty$ che rimane bloccato in uno dei due.
Questo comportamento può anche essere spiegato tornando all’immagine di $F(m)$ precedente. Quando $m \approx 1$ o $m \approx -1$ nell’immagine della simulazione Monte Carlo il sistema sta oscillando attorno ai minimi di $F(m)$. Per passare da $+1$ a $-1$ il sistema ha bisogno di superare una barriera energetica finita, data dalla profondità di $F(\pm 1)$ e quindi l’evento è raro ma non impossibile. In particolare si può dimostrare che la profondità del minimo di $F(m)$ è maggiore quanto maggiore è il numero di spin $N$; perciò per $N$ grande gli eventi di transizione diventano sempre più rari e infine impossibili nel limite $N \to \infty$, dove il sistema rimane bloccato per sempre.
