Un problema apparentemente banale è quello di una matita che cade su un tavolo. In questo contesto una matita è una sbarra sottile con massa uniformemente distribuita. Nonostante la semplicità del problema la combinazione di forze di reazione e attrito renderà possibile un gran numero di comportamenti. Seguiamo Cross, The fall and bounce of pencils and other elongated objects. La situazione è illustrata nell’immagine seguente:
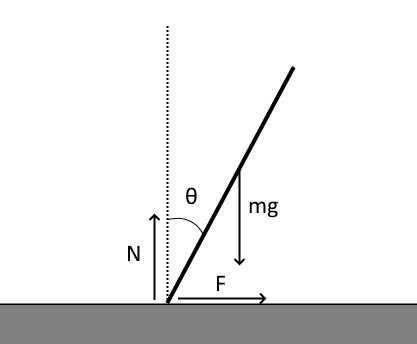
Nell’immagine $N$ è la forza di reazione verticale del tavolo, $F$ è l’attrito, $mg$ è la gravità e $\theta$ l’angolo rispetto alla verticale. Se la matita ha massa $m$ e lunghezza $L$, allora il suo momento d’inerzia rispetto al centro di massa sarà $I = \frac{1}{12} m L^2$. Tipicamente sceglieremmo di considerare il moto angolare rispetto al punto di contatto, ma questa idea diventa complicata nel momento in cui il punto di contatto può muoversi. Le equazioni del moto sono quindi le due equazioni per il moto lungo gli assi $x$ e $y$ e in aggiunta l’equazione del moto angolare. Abbiamo perciò
\begin{align*}
m \dv{v_x}{t} &= F\\
m \dv{v_y}{t} &= N -mg\\
I \dv{\omega}{t} &= N \frac{L}{2} \sin{\theta} -F \frac{L}{2} \cos{\theta}
\end{align*}
dove $v_x$ e $v_y$ sono i componenti della velocità del centro di massa e $\omega = \dv{\theta}{t}$. Supporremo che inizialmente la matita parta da ferma, quindi con $v_x=v_y=\omega=0$ inizialmente e con un angolo $\theta=\theta_0$.
Come sappiamo l’attrito è una forza complicata. In questo caso supporremo per semplicità che i coefficienti di attrito statico e dinamico siano identici. Ora se $F < \mu N$ allora l’attrito è sufficiente a tenere la punta della matita ferma nella direzione orizzontale e quindi il moto sarà puramente rotatorio. Se invece la punta della matita comincia a scivolare, allora avremo $F = \mu N$. Tuttavia l’attrito dipenderà anche dall’angolo a cui si trova la matita: infatti poiché il moto è accelerato ci aspettiamo che $\dv{\omega}{t} > 0$, e quindi dalla terza equazione $F < N \tan\theta$. Perciò ad esempio finché $\tan\theta < \mu$ la matita non potrà scivolare. Man mano che $\theta$ aumenta allora la matita potrà cominciare a scivolare.
Ora supponiamo di aver scelto un angolo $\theta_0$ tale che $\tan\theta_0 < \mu$ e quindi inizialmente la matita sarà bloccata e non potrà scivolare. Finché la matita non scivola avremo quindi $v_x=\omega \frac{L}{2}\cos{\theta}$ e $v_y=-\omega \frac{L}{2}\sin{\theta}$ e quindi le prime due equazioni diventano:
\begin{align*}
m \frac{L}{2} \pqty{\cos\theta \dv{\omega}{t} -\omega^2 \sin\theta} &= F\\
-m \frac{L}{2} \pqty{\sin\theta \dv{\omega}{t} + \omega^2 \cos\theta} &= N -mg
\end{align*}
Possiamo quindi sostituire $F$ e $N$ nella terza equazione ottenendo
$$\frac{1}{3} m L^2 \dv{\omega}{t} = g m \frac{L}{2} \sin{\theta}$$
Questa è la stessa equazione che avremmo ottenuto considerando fisso il punto di contatto della matita, e a quel punto l’unico momento torcente è quello della forza di gravità. È bene aver recuperato quest’equazione, ma ricordiamo che è valida soltanto finché la matita non scivola. In altre parole abbiamo ottenuto $\ddot{\theta} = k^2 \sin{\theta}$ dove $k^2 = 3g/2L$. Il comportamento di questa equazione per $\theta$ piccolo è esponenziale: $\theta \approx \theta_0 \pqty{e^{k t}+e^{-kt}}/2$, e quindi inizialmente l’angolo $\theta$ cresce molto rapidamente. Non siamo in grado di risolvere quest’equazione per $\theta$ generico, ma dalla conservazione dell’energia ricaviamo
$$\omega^2 = 2 k^2 (\cos\theta_0 -\cos\theta) $$
La conservazione dell’energia può essere ottenuta come al solito moltiplicando entrambi i lati dell’equazione del moto per $\omega$ e notando che possono essere entrambi scritti come una derivata rispetto al tempo; quindi abbiamo utilizzato la condizione iniziale per cui $\theta=\theta_0$ e la velocità è nulla. Perciò sostituendo in $N$ e $F$ abbiamo
\begin{align*}
F &=\frac{3}{4} mg \sin\theta \pqty{3\cos\theta -2\cos\theta_0}\\
N &=\frac{1}{4} mg +\frac{3}{4} mg \cos\theta\pqty{3\cos\theta-2\cos\theta_0}
\end{align*}
Come avevamo detto all’inizio questa discussione è valida purché inizialmente l’angolo sia sufficientemente piccolo. Ad un certo punto però $\theta$ aumenterà finché $F=\mu N$ e a quel punto la matita comincerà a scivolare. Per continuare ci poniamo nel caso più interessante in cui la matita è inizialmente quasi verticale, cioè $\cos\theta_0 \approx 1$. In tal caso un grafico illustra bene la situazione:
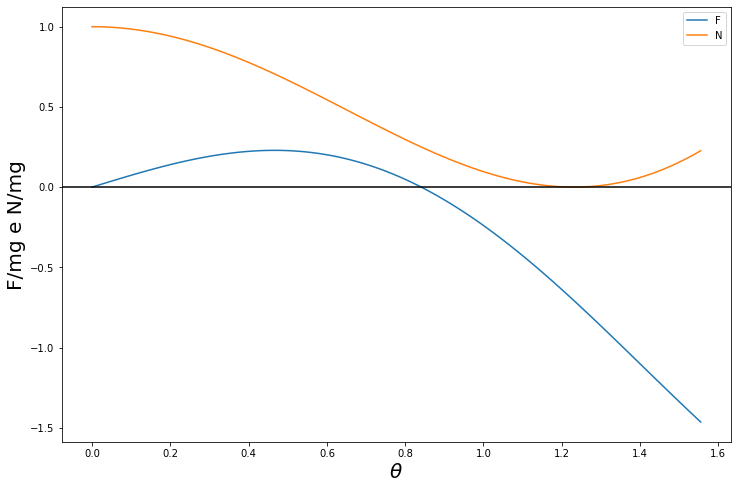
Nel grafico abbiamo le due forze $F$ e $N$ per $0 \leq \theta \leq \frac{\pi}{2}$. Vediamo che inizialmente sia $N$ che $F$ sono positivi e che $N$ è ben maggiore di $F$. Poi ad un certo punto $F$ cambia segno e di lì in poi $N$ rimane piccolo, mente $F$ diventa più grande di $N$. Analiticamente troviamo che $F$ è nulla per $\theta=\cos^{-1}(2/3) \approx 0,84$, mentre $N$ è nulla per $\theta =\cos^{-1}(1/3) \approx 1,23$. Poiché queste espressioni sono state ricavate nell’ipotesi che $F < \mu N$, nel momento in cui ciò accade la matita comincia a scivolare e dobbiamo quindi utilizzare equazioni diverse. Per capire quando ciò accade, consideriamo il rapporto tra le due forze:
\begin{align*}
\frac{F}{N} &=\frac{3\sin\theta \pqty{3\cos\theta -2}}{1 +3\cos\theta\pqty{3\cos\theta-2}}
\end{align*}
che mostriamo nel grafico seguente:
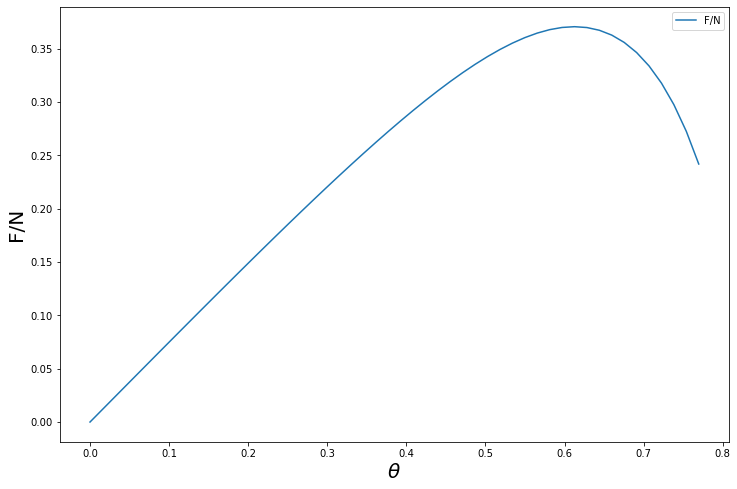
Qui $0 \leq \theta \lesssim \frac{\pi}{4}$ perché per $\theta$ maggiori $N \approx 0$ e quindi il rapporto sarà molto grande e negativo. Il massimo di $F/N$, mostrato in figura, può essere calcolato analiticamente ed è pari a $\frac{15}{64}\sqrt{\frac{5}{2}} \approx 0,37$ nel punto $\theta = 2\tan^{-1}(1/\sqrt{10}) \approx 0,61 \approx \pi/5$.
Per cui abbiamo due casi:
- se $\mu \lesssim 0,37$ allora $\theta$ (che parte da circa $0$) crescerà finché $F/N =\mu$, cosa che avverà nella regione $0 < \theta \lesssim \pi/5$. A questo punto la matita comincerà a scivolare e poiché $F$ è positiva scivolerà all’indietro (la velocità ha il segno opposto della forza d’attrito).
- se invece $\mu \gtrsim 0,37$ allora per tutta la regione $0 < \theta < \pi/4$ nell’immagine precedente avremo $F < \mu N$. Tuttavia poiché poi $N$ diminuisce fino a zero mentre $F$ continua a crescere in valore assoluto, allora da qualche parte nella regione $0,89 \lesssim \theta \lesssim 0,94$ necessariamente avremo $F=\mu N$ in valore assoluto, come illustrato nella figura seguente. Tuttavia in questo caso $F$ è negativa, e quindi sorprendemente la matita scivolerà in avanti.
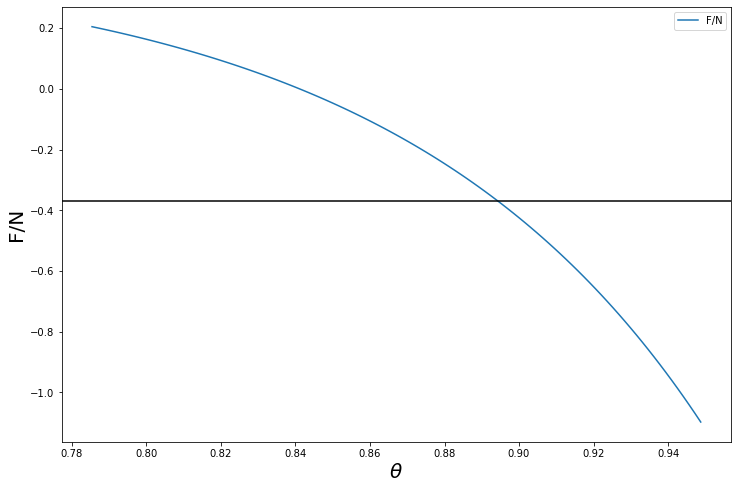
La linea nera nell’immagine rappresenta $\mu \approx 0,37$.
È anche interessante notare che l’angolo di inizio dello scivolamento salta improvvisamente passando da sopra a sotto di $\mu \approx 0,37$. Infatti approcciando il valore critico dell’attrito da sotto, l’angolo di scivolamento cresce in maniera continua da $0$ fino al massimo di $F/N$, ovvero $\theta = 2\tan^{-1}(1/\sqrt{10}) \approx 0,61 \approx 35^\circ$. Al contrario approcciando l’attrito critico da sopra, per $\mu \approx 1$ l’angolo di scivolamento sarà circa $\theta \approx 0,94 \approx 54^\circ$, mentre scendendo verso $\mu \approx 0,37$ l’angolo diventa $\theta=2\tan^{-1}\pqty{\frac{2\sqrt{14}-9}{\sqrt{10}}} \approx 0,89 \approx 51^\circ$. Riassumendo, aumentando l’attrito da $\mu=0$ a $\mu \approx 37^\circ$ l’angolo di scivolamento aumenta continuamente da $0^\circ$ a $35^\circ$, mentre aumentando ancora $\mu$ l’angolo salta e va da $51^\circ$ a $54^\circ$, un intervallo molto ristretto. Notiamo che i due casi sono anche distinti qualitativamente: per $\mu$ piccolo lo scivolamento è all’indietro, mentre per $\mu$ grande è verso avanti. Nel limite in cui $\mu=0$ l’angolo di scivolamento è $0^\circ$, e infatti in quel caso il tavolo non può trattenere la matita, su cui non agiscono forze orizzontali: perciò il centro di massa cade verticalmente seguendo la gravità.
Una volta che la matita inizia a scivolare l’equazione per $N$ rimane valida, mentre $F$ viene ora ricavata tramite $F=\mu N$:
\begin{align*}
\mu N &= F\\
-m \frac{L}{2} \pqty{\sin\theta \dv{\omega}{t} + \omega^2 \cos\theta} &= N -mg
\end{align*}
A questo punto sostituendo nella terza equazione otteniamo l’equazion del moto
$$\dv{^2\theta}{t^2} = \frac{3\pqty{\frac{2g}{L}-\dot{\theta}^2 \cos\theta}\pqty{\sin\theta-\mu\cos\theta}}{1+3\sin\theta(\sin\theta-\mu\cos\theta)} $$
Inutile dire che questa equazione è insolubile se non numericamente. A tal scopo dobbiamo iniziare con l’equazione valida nel caso senza scivolamento fino all’angolo per cui abbiamo $F=\mu N$. A quel punto otterremo dei valore di $\theta$ e $\dot{\theta}$ che serviranno come condizioni iniziali per quest’ultima equazione.
