La distinzione tra transizioni del primo e del second’ordine è ben nota in fisica statistica. In una transizione del prim’ordine, il parametro d’ordine è discontinuo, mentre invece è continuo in una transizione del second’ordine. Un’altra distinzione importante è che la lunghezza di correlazione è infinita ad una transizione del second’ordine, mentre invece rimane finita in una transizione del prim’ordine. Perciò, come abbiamo visto, un modello su reticolo ha un limite del continuo solo se ha una transizione del second’ordine.
Ora vediamo cosa succede nel formalismo Hamiltoniano. Data una funzione di partizione classica $Z$ possiamo trovare uno spazio di Hilbert e un’Hamiltoniana tali che $Z = \tr\pqty{e^{-\beta H}}$. Una connessione importante tra i due formalismi è che la lunghezza di correlazione del sistema classico è l’inversa del divario energetico quantistico, $\xi \sim 1/\Delta^z$ dove $z > 0$ è un qualche esponente. Ciò significa in particolare che ad una transizione del prim’ordine il gap rimane finito, mentre si chiude (diventa nullo) in una transizione del second’ordine.
In maniera più esplicita, consideriamo un’Hamiltoniana della forma $H = H_0 + g H_1$ al variare di $g$. Una possibilità è ci sia un incrocio di livelli energetici, cioè che ad un certo punto la natura dello stato fondamentale cambi:
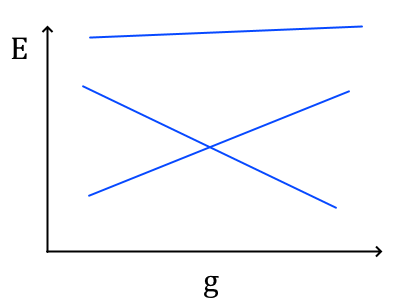
Ovvero ad un certo punto speciale $g= g_c$ uno stato che prima era eccitato diventa lo stato fondamentale. Ciò però in linea di massima non succede, quantomeno in una situazione di volume finito. Infatti a meno che $H_0$ e $H_1$ non commutino, una perturbazione di $H_0$ con $H_1$ tenderà a separare i livelli energetici. Se invece $H_0$ e $H_1$ commutano, sono simultaneamente diagonalizzabili e quindi gli autovettori non dipenderanno da $g$; allora è possibile che i due livelli energetici si incrocino, ma la situazione non è molto interessante. Ciò che invece succede in maniera generica è un cosiddetto incrocio evitato, cioè una situazione del genere:
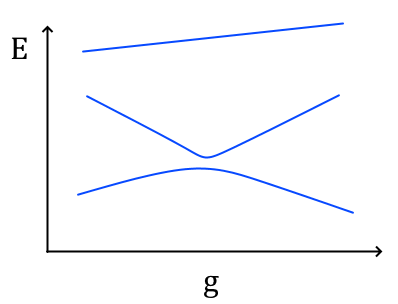
In particolare, i due stati arrivano molto vicini ma non si scambiano e non c’è nessun incrocio. Ciò in generale è ciò che avviene a volume finito. Aumentando il volume abbiamo diverse possibilità:
- L’incrocio rimane evitato. Cioè aumentando il volume, gli stati diventano molto vicini l’uno con l’altro, ma lo stato fondamentale rimane lo stesso. In questo caso non c’è nessuna transizione di fase.
- Un numero finito di stati si incrocia. In tal caso aumentando il volume, gli stati si avvicinano sempre di più fino a scambiarsi; questa è la situazione mostrata nella prima figura con due stati, ma può accadere anche con tre o più stati. Ora lo stato fondamentale cambia natura al punto di transizione, e al punto stesso c’è coesistenza tra le due fasi. Abbiamo quindi una transizione del prim’ordine.
- Un numero infinito di stati si forma sopra al punto di transizione. In questo caso, si accumulano infiniti stati sopra al punto di transizione, e quindi il divario energetico si chiude: basta un’energia arbitrariamente piccola per eccitare uno stato. Abbiamo quindi una transizione del second’ordine.
In volume infinito una transizione del prim’ordine avrà uno spettro del genere:
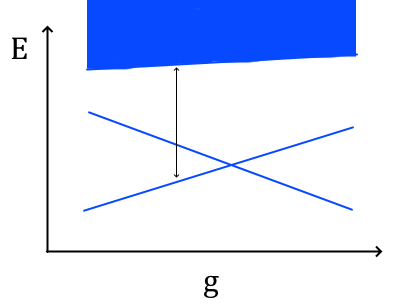
Ovvero anche se lo stato fondamentale è sempre unico e non-degenere tranne al punto di transizione, moralmente abbiamo due “stati fondamentali” che rappresentano due fasi possibili del sistema che si scambiano il ruolo di stato fondamentale vero e proprio al punto di transizione. Ad un certo punto avremo un continuo di stati, rappresentato dal blu pieno, che però non può essere raggiunto a partire dagli stati fondamentali con energie arbitrariamente basse: perciò il sistema ha un divario energetico, indicato in figura, e ciò è coerente con il fatto che per una transizione del prim’ordine la lunghezza di correlazione è finita.
Ad una transizione del second’ordine, invece, sempre a volume infinito, la situazione è rappresentata dalla figura seguente:
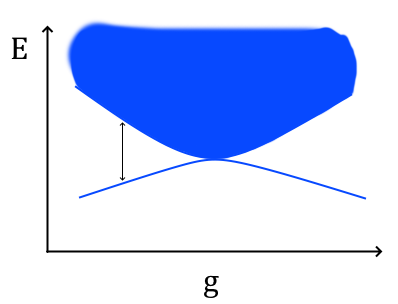
In questo caso il divario energetico (indicato in figura) diventa nullo al punto di transizione: un’energia arbitrariamente piccola è sufficiente ad eccitare degli stati. In questo caso al punto di transizione la lunghezza di correlazione è quindi infinita. In realtà abbiamo anche un’altra possibilità, come nella figura seguente:
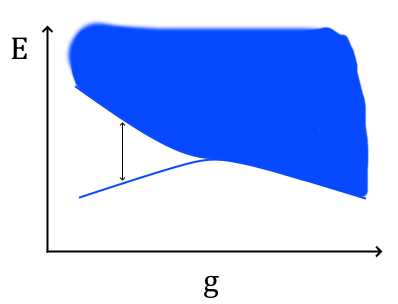
Ovvero ad un certo punto il divario energetico si chiude e quindi abbiamo una transizione del second’ordine. Dopo la transizione, però, il divario energetico rimane nullo: ciò succede, ad esempio, quando abbiamo rottura spontanea di una simmetria continua in dimensione maggiore di $2$. In tal caso abbiamo i cosiddetti bosoni di Goldstone, che sono appunto delle eccitazioni a massa nulla. Perciò hanno divario energetico nullo.
Concludiamo mostrando gli stati di un sistema che abbiamo risolto esattamente il passato, cioè il modello di Ising quantistico in una dimensione, con Hamiltoniana
$$H = -\sum_{i} \sigma_i^z \sigma_{i+1}^z-g \sum_i \sigma_i^x$$
In questo caso i livelli energetici rispetto allo stato fondamentale sono dati da
$$E(k)-E_0 = 2\sqrt{1+g^2-2g\cos{k})}$$
dove $k = 2\pi n / N$ per $n=0,1,\ldots, N-1$ dove $N$ è il numero di siti. Il numero di stati è quindi finito in volume finito, ma infinito nel limite $N \to \infty$. I livelli energetici sono plottati per $N=10$ e $N=100$ nelle due figure seguenti:
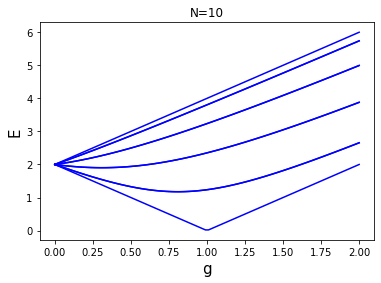
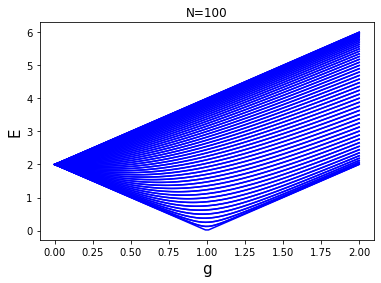
L’energia è rispetto allo stato fondamentale (che ha essenzialmente energia arbitraria). Vediamo che il divario energetico si chiude per $g=1$ come previsto. In questo caso andando nel limite di volume infinito $N \to \infty$ vediamo esplicitamente che gli stati formano un continuo sopra il punto critico. La transizione è quindi del second’ordine.
