Consideriamo un reticolo ipercubico periodico in D dimensioni, con una lunghezza (numero di siti) Ni nella direzione i. Molto spesso torna utile calcolare il numero di vari elementi (archi, placchette) del reticolo. Questa operazione è molto semplice una volta trovato il modo giusto di affrontare la cosa, e altrimenti può essere molto difficile.
La cosa più semplice è il numero di siti, data semplicemente da N1N2⋯ND, cioè il prodotto delle lunghezze nelle D direzioni.
Come esempio non banale, consideriamo invece gli archi. Un arco collega due siti primi vicini, ed è perciò definito da un sito →x e da una direzione μ. Per definizione l’arco collegherà quindi il sito →x col sito →x+μ. Poiché abbiamo condizioni al contorno periodiche, allora tutti gli archi così definiti sono validi. Perciò il numero degli archi sarà DN1N2⋯ND, ovvero ne abbiamo D per sito.
Per le placchette la situazione sarà simile. Infatti una placchetta è definita da un sito e poi dalla scelta di due direzioni in cui emana. In D dimensioni possiamo scegliere (D2)=D(D−1)/2 direzioni, ovvero 0 in una dimensione, 1 in due dimensioni, 3 in tre dimensioni, 6 in quattro dimensioni e via dicendo. Perciò abbiamo un totale di 12D(D−1)N1N2⋯ND placchette.
In generale, una struttura base d-dimensionale sarà definita per ogni sito dalla scelta di d dimensioni tra le D disponibili, e perciò ne avremo (Dd) per sito. Ad esempio il numero di cubi unitari corrisponde a d=3.
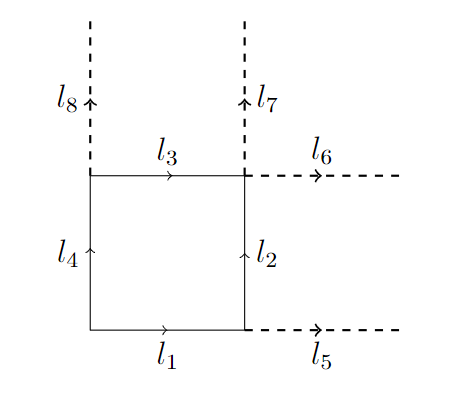
Possiamo controllare che il conteggio è corretto in alcuni casi semplici. In una dimensione con N siti, abbiamo effettivamente N archi e zero placchette. In due dimensioni, l’immagine mostra ad esempio un reticolo 2×2 con condizioni al contorno periodiche quindi con 4 siti, 8 archi e 4 placchette.
