I mesoni sono delle particelle formate dalla coppia di un quark e un antiquark. Un’osservazione interessante è che per ogni mesone, disegnando il grafico della massa al quadrato $m^2$ in relazione allo spin $J$, troviamo che diverse famiglie di mesoni si dispongono su linee rette dette traiettorie di Regge:
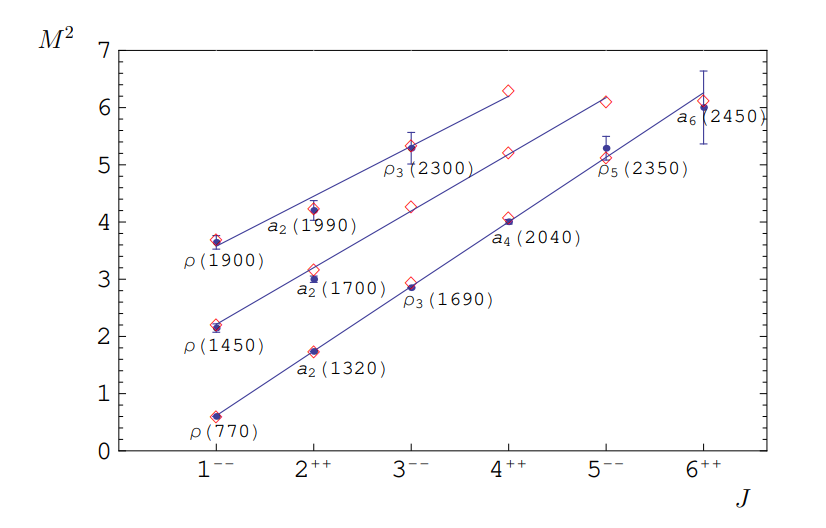
Presa da questo articolo.
Nell’immagine abbiamo lo spin totale $J$ e la massa al quadrato $M^2$ per i mesoni $\rho$ e $a$ e i loro stati eccitati. Entrambi i mesoni sono formati da un quark $u$ e da un quark $d$, mentre la notazione $J^{PC}$ indica lo spin $J$ e il segno rispetto alla parità e alla coniugazione di carica. Notiamo che tutti i $\rho$ hanno $PC=–$ mentre tutti gli $a$ hanno $PC=++$. Il numero tra parentesi è l’energia associata allo stato.
Questo comportamento può essere ricavato da un modello molto semplice per cui un mesone è formato da un quark e un antiquark collegati da una corda relativistica. L’idea è che questa corda altro non sia se non il flusso del campo di forza cromodinamico che per qualche motivo, invece di espandersi è collimato in “tubo” tra i due quark. La corda sarebbe appunto il tubo del campo cromodinamico. L’idea è illustrata nella figura seguente:
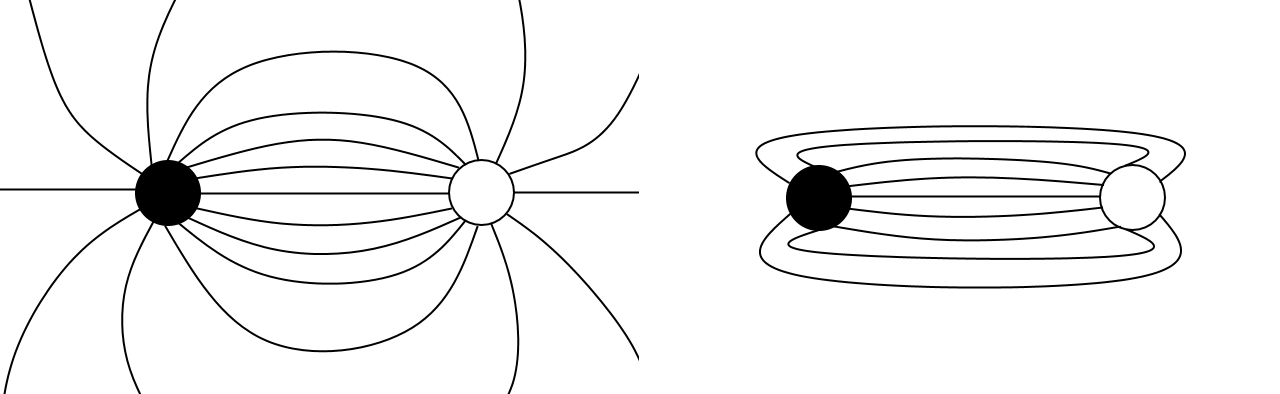
Possiamo trovare un’analogia con un dipolo magnetico in un superconduttore. Supponiamo che esistano dei monopoli magnetici, cioè delle particelle con carica magnetica. Nello stato di conduzione normale, un dipolo, cioè una coppia di carica magnetica positiva e negativa, avrà il campo solito di un dipolo, mostrato nell’immagine a sinistra. Quando invece entriamo nello stato superconduttivo, per effetto Meissner il campo magnetico all’interno del superconduttore viene soppresso e l’unica cosa che rimane è un tubo collimato tra i due monopoli magnetici, mostrato nell’immagine a destra.
Detto ciò, proviamo a derivare le traiettorie di Regge. Supponiamo i due quark attaccati alla corda abbiano massa nulla. La corda avrà densità di energia per unità di lunghezza pari a $\sigma$. Supponiamo che la corda sia completamente tesa e ruoti a velocità angolare costante in modo che la velocità dei quark sia pari alla velocità della luce. In questo senso il centro della corda è in $r=0$, e si estende fino a $r=R$ per una lunghezza totale di $L=2R$. La velocità angolare della corda $\omega$ è costante, e la velocità è quindi uguale a $v(r)=\omega r$. Poiché sappiamo che i quark ruotano alla velocità della luce, $v(R)=c$ e quindi $\omega=c/R$. Pertanto $v(r) = c r / R$. Un elemento infinitesimale di corda avrà quindi energia $dE = \gamma \sigma dr$ e quindi l’energia totale della corda sarà
$$E = 2 \int_0^R \frac{\sigma dr}{\sqrt{1-r^2/R^2}} = \pi \sigma R$$
Il momento angolare infinitesimale sarà invece $dJ = r v(r) \gamma \sigma dr$ e quindi
$$J = 2 \int_0^R \frac{\sigma r^2dr}{R\sqrt{1-r^2/R^2}} = \frac{\pi}{2} \sigma R^2$$
Poiché $E=M$ abbiamo quindi
$$\boxed{M^2 = 2\pi \sigma J}$$
Perciò per tutti i mesoni dovremmo avere delle traiettorie di Regge con lo stesso coefficiente angolare $2\pi \sigma$, che è appunto una proprietà della stringa, cioè del campo cromodinamico, cosa che effettivamente osserviamo.
Notiamo inoltre che abbiamo ottenuto il risultato secondo cui l’energia di una coppia di quark-antiquark cresce linearmente con la loro separazione $R$. Ciò vuol dire che se provassimo a separare la coppia, l’energia aumenterebbe finché ad un certo punto supererebbe la soglia di due masse dei quark fondamentali, cioè diventerebbe abbastanza grande da creare un’altra coppia quark-antiquark. In tal caso invece di separarsi, i due quark formerebbero due coppie quark-antiquark ravvicinate, cioè due mesoni. Questo comportamento è la causa del confinamento dei quark: provando a separarli “rompiamo la stringa” e formiamo invece due mesoni, perciò non possiamo mai osservare dei quark liberi.
Abbiamo visto che questo semplice modello cattura le caratteristiche essenziali delle traiettorie di Regge, ma rimane comunque molto basilare: ad esempio già nella prima figura vediamo che le rette hanno sì lo stesso coefficiente angolare, ma intercetta diversa. Nel nostro modello l’intercetta è del tutto assente e quindi il modello non riesce a catturare questo aspetto del comportamento dei mesoni. Inoltre l’approssimazione ultrarelativistica secondo cui i quark si muovono alla velocità della luce è valida solo per i quark con massa più piccola. È tuttavia possibile sviluppare questa teoria in maniera sistematica, ottenendo le correzioni alla semplice legge che abbiamo qui derivato, ottenendo cioè una “teoria delle stringhe” del tutto analoga a quella più famosa, ma in questo contesto non è una teoria del tutto, quanto piuttosto una teoria efficace del comportamento dei quark.
