La teoria quantistica dei campi è notoriamente molto difficile. La teoria $\phi^4$ è tra le teorie quantistiche interagenti più semplici e viene spesso utilizzata come giocattolo per modelli più interessanti. In questa serie di articoli consideriamo un caso particolarmente semplice, cioè la teoria $\phi^4$ in $0$ dimensioni spaziotemporali. Questa teoria illustrerà alcune caratteristiche generali delle teorie quantistiche dei campi.
In $d$ dimensioni spaziotemporali un campo scalare reale è una funzione $\phi : \R^d \to \R$. Nel caso in cui $d=0$, cioè lo spaziotempo è ridotto ad un solo punto, il campo scalare è una mappa da un punto ad $\R$, cioè è semplicemente una variable reale $\phi \in \R$. Poiché $d=0$ non abbiamo neanche le derivate, e quindi l’azione Euclidea della teoria è data semplicemente dal potenziale:
$$S[\phi] = \frac{1}{2} \phi^2 + \frac{g}{4!}\phi^4$$
In questo caso non ha senso moltiplicare $\phi^2$ per una massa $m^2$ perché possiamo rimuoverla semplicemente ridefinendo il campo $\phi$. L’oggetto che ci interessa è l’integrale sui cammini, che in questo caso è un integrale ordinario:
$$Z[g] = \int_{\R} \frac{d\phi}{\sqrt{2\pi \hbar}}\, \exp{\bqty{-\frac{1}{\hbar}\pqty{\frac{1}{2} \phi^2 + \frac{g}{4!}\phi^4}}}$$
Poiché questo è un integrale ordinario e quindi è ben definito, possiamo studiarne le proprietà in una maniera che sarebbe impossibile per altre teorie dei campi.
In questo articolo vediamo la cosa più semplice che possiamo calcolare, cioè la serie perturbativa. Al solito in teoria dei campi utilizziamo i diagrammi di Feynman, ma qui possiamo effettuare il calcolo in maniera anche più semplice. Esattamente come in teoria dei campi, espandiamo il termine di interazione nell’integrale sui cammini e integriamo termine per termine:
\begin{align*}
Z[g] &= \int_{\R} \frac{d\phi}{\sqrt{2\pi \hbar}}\, \exp{\bqty{-\frac{1}{\hbar}\pqty{\frac{1}{2} \phi^2 + \frac{g}{4!}\phi^4}}}=\\
&= \int_{\R} \frac{d\phi}{\sqrt{2\pi \hbar}}\, e^{-\frac{1}{2\hbar}\phi^2} \sum_{n=0}^\infty \frac{1}{n!} \pqty{-\frac{g}{4! \hbar}\phi^4}^n=\\
&=\sum_{n=0}^\infty \frac{1}{n!} \pqty{-\frac{g}{4! \hbar}}^n \int_{\R} \frac{d\phi}{\sqrt{2\pi \hbar}}\, e^{-\frac{1}{2\hbar}\phi^2} \phi^{4n}=\\
&=\sum_{n=0}^\infty \frac{ (4n-1)!! }{n!} \pqty{-\frac{\hbar g}{24}}^n
\end{align*}
Andando dalla seconda alla terza riga abbiamo effettuato un passaggio illegale, cioè abbiamo scambiato una serie con un integrale. Dalla terza alla quarta riga abbiamo usato l’integrale Gaussiano
$$\int_{-\infty}^{+\infty} dx\, x^{2m} e^{-\frac{x^2}{a^2}} = \sqrt{\pi} \frac{a^{2m+1} (2m-1)!!}{2^{m}}$$
Per $m=0$ la formula ha un problema perché dovremmo calcolare il fattoriale doppio di $-1$. Vediamo che ponendo per definizione $(-1)!!=1$ tutte le formule restano corrette.
Abbiamo quindi ottenuto una rappresentazione di $Z(g)$ in una serie in $g$, esattamente analoga alla serie perturbativa di una solita teoria dei campi. Poiché al contrario del solito conosciamo tutti i termini di questa serie possiamo calcolarne il raggio di convergenza nella variabile di espansione $g\hbar$:
$$R = \lim_{n\to \infty} \abs{\frac{a_n}{a_{n+1}}}=24\lim_{n\to \infty}\frac{(n+1)}{ (4n+3)(4n+1) }=0$$
Ovvero per ogni valore finito di $g$ (o di $g\hbar$), la serie è divergente. Questo comportamento era già stato predetto da Dyson per l’elettrodinamica quantistica, come abbiamo visto in un precedente articolo. In altri termini la serie è soltanto una serie asintotica: prendendo i primi $N$ termini con $N$ fisso, la serie si avvicina a $Z(g)$ tanto più $g$ è piccolo; tuttavia per qualsiasi $g$ finito se sommiamo tutti i termini (cioè mandiamo $N \to \infty$) allora la serie diverge.
Tipicamente i termini di una serie asintotica diventano sempre più piccoli all’inizio, poi ad un certo punto cominciano a crescere e diventano sempre più grandi fino a divergere. Il fenomeno è illustrato nella figure seguenti:
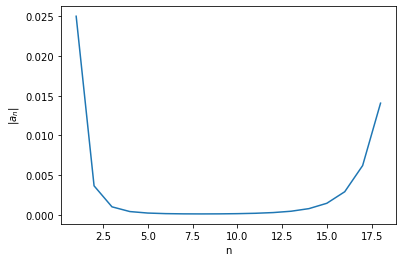
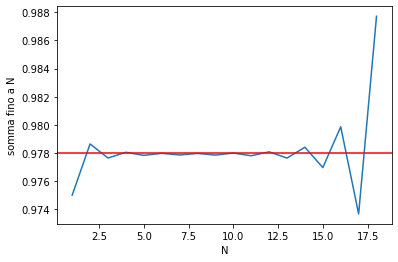
In entrambe le immagini abbiamo fissato $g\hbar = 0,2$. La prima immagine mostra il valore assoluto dei termini della serie da $n=2$ in poi. All’inizio il termine esponenziale $(-g\hbar/24)^n$ domina e quindi i termini decrescono, poi il rapporto di fattoriali domina e quindi ad un certo punto i termini diventano sempre più grandi e tendono all’infinito per $n \to \infty$. Nella seconda immagine invece è data in blu la somma dei primi $N$ termini della serie, mentre in rosso è dato il valore esatto di $Z$ calcolato numericamente. Come vediamo all’inizio la serie approssima il valore esatto sempre meglio, fino ad una regione centrale in cui l’approssimazione è ottima; poi però i termini successivi tendono a discostarsi dal valore corretto e come abbiamo detto prima sommando tutti i termini della serie otteniamo infinito.
Possiamo anche stimare qual è il numero ottimale di termini da sommare. In particolare il numero ottimale di termini $N$ sarà ottenuto quando il termine $N$-esimo della serie sarà il più piccolo possibile. Utilizzando la formula esplicita per il fattoriale doppio e l’approssimazione di Stirling abbiamo:
$$\log{\bqty{\frac{ (4n-1)!! }{n!} \pqty{\frac{\hbar g}{24}}^n}}\approx n\log{n}-n +4n\log{2}+n\log{\pqty{\frac{\hbar g}{24}}}$$
Poiché il logaritmo è monotono crescente, possiamo minimizzare direttamente il logaritmo. Calcolando la derivata rispetto ad $n$ e ponendola uguale a zero otteniamo che il minimo si ottiene quando
$$n \approx \frac{3}{2 g\hbar}$$
Nell’esempio precedente avevamo $g\hbar=0,2$ per cui il minimo dovrebbe trovarsi a circa $n \approx 8$, numero confermato dal grafico della funzione. Notiamo in particolare che per $g$ piccolo il numero ottimale di termini è molto elevato e quindi possiamo raggiungere un’elevata precisione; mentre invece per $g$ relativamente grande il numero di termini ottimale è molto piccolo e non possiamo aspettarci che la serie perturbativa che abbiamo ottenuto dia risultati significativi. Questo comportamento è del tutto generico per una serie asintotica, e infatti la serie che abbiamo derivato è valida solo per $g$ piccolo o “interazioni deboli”.
Nel prossimo articolo della serie vediamo un altro tipo di serie perturbativa per lo stesso modello.
