Consideriamo il modello di Ising con $N$ spin classici in una dimensione, con Hamiltoniana “ridotta”
\begin{equation*}
H = h \sum_i s_i + K \sum_{i} s_i s_{i+1} + CN
\end{equation*} dove abbiamo introdotto una costante $C$ per convenienza futura e con “ridotta” intendiamo che abbiamo assorbito un fattore di $-\beta$ nelle costanti, così che la funzione di partizione è:
\begin{equation*}
Z = \prod_{i} \pqty{\frac12 \sum_{s_i=\pm 1}} e^{H(\{s_i\})}
\end{equation*}il fattore di $1/2$ normalizza correttamente la somma sui due valori dello spin ma è arbitraria perché semplicemente una costante moltiplicativa davanti alla funzione di partizione.
Nel caso di un modello su reticolo, per rinormalizzazione intendiamo effettuare uno “zoom al contrario“, in modo da guardare il modello da un punto di vista sempre più lontano. Questa tecnica di rinormalizzazione viene detta “a blocchi di spin” o anche “decimazione” e ad ogni passo consiste nel “combinare” insieme due spin vicini ottenendone uno solo risultante. In questa maniera, ad ogni passo riduciamo di metà il numero degli spin e procedendo all’infinito (dove supponiamo anche infinito il numero degli spin) otteniamo lo “zoom al contrario” che volevamo.
In pratica, nella funzione di partizione $Z$ effettuiamo la somma su spin alterni, cioè ne “integriamo” via uno sì e uno no, in modo che uno spin viene sommato e i suoi vicini rimangono al loro posto. In questa maniera uno spin su due è integrato via, e rimarrà alla fine la funzione di partizione per gli spin che rimangono, cioè la metà di quelli iniziali. Supponiamo che uno spin $s$ abbia per vicini $s_-$ e $s_+$. Vogliamo effettuare la somma su $s$, in maniera che $s$ non appaia più nella funzione di partizione. Una volta fatto ciò per spin alterni, saremo rimasti con la funzione di partizione per una catena di $N/2$ spin, in cui però la distanza tra due spin primi vicini è raddoppiata. Che funzione di partizione otteniamo? Consideriamo $s$, $s_-$ e $s_+$. Ci interessano in $Z$ i termini in cui compare $s$:
\begin{equation*}
\pqty{\cdots} \pqty{\frac12 \sum_{s=\pm 1}} e^{\frac12 h (s_-+s) + K s s_- + C} e^{\frac12 h (s_++s) + K s s_+ + C}
\end{equation*} dove i pallini stanno a indicare tutti gli altri termini nella funzione di partizione. Quest’ultima espressione può essere scritta come
\begin{equation*}
\pqty{\cdots} e^{\frac12 h (s_-+s_+) + 2C} \pqty{\frac12 \sum_{s=\pm 1}} e^{s \bqty{h + K (s_- + s_+)}}
\end{equation*} Ora possiamo “integrare” $s$ ottenendo
\begin{equation*}
\pqty{\cdots} e^{\frac12 h (s_-+s_+) + 2C} \cosh{\pqty{h + K (s_- + s_+)}}
\end{equation*} Ora, $s_-+s_+$ può prendere solo tre valori: $0,\pm 2$. Provando tutte le varie possibilità, vediamo che quest’ultima formula è uguale a
\begin{equation*}
\pqty{\cdots} e^{\frac12 h’ (s_-+s_+) + K’ s_+ s_- + C’}
\end{equation*} dove
\begin{align*}
h’ &= h + \frac12\log{\cosh{\pqty{h+2K}}}-\frac12\log{\cosh{\pqty{h-2K}}}\\
K’ &= \frac14\log{\cosh{\pqty{h+2K}}}+\frac14\log{\cosh{\pqty{h-2K}}} -\frac12 \log{\cosh{h}}\\
C’ &= 2C +\frac14\log{\cosh{\pqty{h+2K}}}+\frac14\log{\cosh{\pqty{h-2K}}} + \frac12 \log{\cosh{h}}
\end{align*} Effettuando questa stessa procedura per uno spin sì e uno no, otteniamo
\begin{equation*}
Z = \prod_{i\,\mathrm{pari}} \pqty{\frac12 \sum_{s_i=\pm 1}} e^{H'(\{s_i\})}
\end{equation*} dove $H’$ ha la stessa forma di $H$, ma con parametri diversi, $h’=h'(h,K)$, $K’=K'(h,K)$ e $C’ = 2C+\widetilde{C}'(h,K)$. La cosa incredibile è che alla fine di tutta questa procedura complicata abbiamo ottenuto la stessa Hamiltoniana, solo con parametri diversi. Tuttavia questa nuova teoria è del tutto equivalente alla teoria iniziale, poiché la funzione di partizione rimane identica.
Traiettorie di rinormalizzazione
A questo punto possiamo effettuare un nuovo passo di rinormalizzazione, integrando via di nuovo spin alterni. Questa procedura è esattamente identica a quella che abbiamo appena effettuato, per cui otterremo di nuovo la stessa Hamiltoniana con dei nuovi parametri $h^{\prime\prime}$, $K^{\prime\prime}$, $C^{\prime\prime}$ dati dalle stesse equazioni di prima. Possiamo continuare questo gioco all’infinito, ottenendo una serie infinita di teorie equivalenti con parametri diversi. La sequenza di questi parametri mostra un “flusso di rinormalizzazione“, come mostrato nella figura seguente:
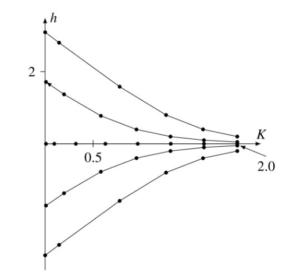
In questo caso ignoriamo $C$ perché è solo una costante additiva. Partendo da certi parametri iniziali $h,K$ ed effettuando una decimazione dopo l’altra all’infinito, vediamo che $h \to 0$ e $K \to \infty$. Infatti le equazioni sopra hanno due punti fissi: uno dato da $h=0, K=0$ oppure il punto fisso $h=0, K = \infty$. Una volta raggiunto un punto fisso, ulteriori passi di rinormalizzazione non cambieranno più la teoria. Ora poiché abbiamo assorbito la temperatura inversa $\beta$ nelle costanti di accoppiamento, sappiamo che il limite di alta temperatura corrisponde a $K$ piccolo, e quindi il punto fisso a $K=0$ descrive gli spin completamente disaccoppiati che oscillano in maniera del tutto casuale. Al contrario $K=\infty$ corrisponde al limite di temperatura nulla in cui gli spin sono tutti allineati.
La lunghezza di correlazione
In questo caso abbiamo tralasciato un dettaglio importante. Se inizialmente la distanza tra due spin primi vicini è $a$, dopo aver eliminato metà degli spin la distanza tra due primi vicini è $2a$. Se vogliamo dire che la nostra teoria è rimasta invariata, tranne che per la variazione dei parametri, allora dobbiamo riscalare la catena di un fattore di un $1/2$ in modo che la distanza tra due primi vicini sia di nuovo $a$. In questo modo, dopo la rinormalizzazione la teoria è veramente identica a prima, tranne appunto per la variazione dei parametri. In questo caso questo passo non cambia l’Hamiltoniana, ma in una teoria del continuo lo farebbe ed è meglio non dimenticarsene.
Ora la lunghezza di correlazione $\xi$ è definita come
$$\langle s_i s_j \rangle = e^{-\abs{i-j}/\xi}$$
Poiché ad ogni passo riscaliamo la catena, dopo ogni passo la lunghezza di correlazione viene dimezzata $\xi’ = \frac{\xi}{2}$. Pertanto ad un punto fisso avremo $\xi=0$ oppure $\xi=\infty$. Sappiamo che $K=0$ corrisponde al limite di alta temperatura: in quel caso gli spin oscilleranno tutti casualmente e indipendentemente dagli altri, e quindi avremo $\xi = 0$. Al contrario per $K=\infty$ gli spin sono tutti allineati e quindi tutti correlati: la lunghezza di correlazione sarà perciò $\xi = \infty$.
