Abbiamo visto in uno scorso articolo che è possibile definire una funzione di correlazione per dei “difetti” nel modello di Ising in 2D. Questi fungono da parametri di disordine per il modello, nel senso che hanno fasi opposte rispetto alle solite variabili di spin $\sigma$: quando una è ordinata, l’altra è disordinata e viceversa.
Nonostante avessimo definito la funzione di correlazione $\langle \mu(\widetilde{\boldsymbol{r}}) \mu(\widetilde{\boldsymbol{r}}’) \rangle$ per i difetti $\mu$, la definizione richiedeva in realtà la scelta di un cammino $\Gamma$ tra $\widetilde{\boldsymbol{r}}$ e $\widetilde{\boldsymbol{r}}’$. Rimandiamo all’articolo precedente per la definizione. Qui dimostriamo che in realtà questa funzione di correlazione dipende solo dai punti di partenza e fine del cammino, e quindi i parametri di disordine $\mu$ hanno vita indipendente.
Torna utile utilizzare il linguaggio della teoria di calibro (“gauge“). Introduciamo un campo di calibro $\tau_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} = \pm 1$ definito su ogni collegamento $\langle\boldsymbol{r}, \boldsymbol{r}’\rangle$ tra due siti primi vicini del reticolo. L’Hamiltoniana è data da
$$H_\Gamma = -J \sum_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} \sigma(\boldsymbol{r}) \tau_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} \sigma(\boldsymbol{r}’)$$
dove $\tau$ è un campo prefissato. Senza il difetto $\tau=+1$ dappertutto, mentre invece con l’introduzione del difetto $\Gamma$ avremo $\tau=-1$ in quei collegamenti che intersecano $\Gamma$. Abbiamo una simmetria di calibro, cioè una simmetria locale: mandando $\sigma(\boldsymbol{r}) \to \lambda(\boldsymbol{r}) \sigma(\boldsymbol{r})$ dove $\lambda(\boldsymbol{r}) = \pm 1$ è in linea di principio diversa in ogni sito, l’Hamiltoniana è invariata se abbiamo anche la trasformazione di calibro per il campo esterno data da $\tau_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} \to \lambda(\boldsymbol{r})\tau_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle}\lambda(\boldsymbol{r}’)$.
Come sempre in una teoria di calibro è utile introdurre l’operatore di Wilson
$$W_\gamma = \prod_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle \in \gamma}\tau_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} $$
dove $\gamma$ è un qualsiasi cammino chiuso sul reticolo. Anche questo operatore è invariante di calibro, cioè è invariante rispetto alla trasformazione locale definita sopra. Il più piccolo cammino chiuso sul reticolo è il quadratino formato da quattro collegamenti, detto placchetta. L’operatore di Wilson ci permette di inviduare la posizione dei difetti $\mu(\widetilde{\boldsymbol{r}})$. Infatti notiamo che $W_\gamma = -1$ se $\gamma$ racchiude esattamente uno dei difetti $\mu$ che danno origine a $\gamma$, altrimendi $W_\gamma = +1$. La situazione è illustrata nella stessa figura dell’altra volta:
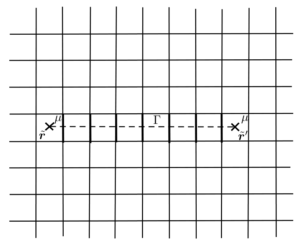 Consideriamo l’esempio in cui $\gamma$ è una placchetta. Se $\gamma$ non c’entra niente con il cammino $\Gamma$ tra i difetti, allora per tutti e quattro i collegamenti in $\gamma$ avremo $\tau = +1 $ e quindi in totale $W_\gamma = +1$. Consideriamo invece il caso in cui $\gamma$ è quadratino (placchetta) che racchiude uno tra $\widetilde{\boldsymbol{r}}$ e $\widetilde{\boldsymbol{r}}’$ (che appunto, in quanto siti del reticolo duale, sono al centro di quadratini del reticolo originale). In questo caso tre dei collegamenti in $\gamma$ hanno $\tau = +1$, mentre uno ha $\tau = -1$ e quindi in totale $W_\gamma = -1$. L’ultimo caso è quello in cui $\gamma$ è una placchetta che interseca $\Gamma$: in questo caso avremo due collegamenti con $+$ e due con $-$, per cui in totale $W_\gamma = +1$ di nuovo.
Consideriamo l’esempio in cui $\gamma$ è una placchetta. Se $\gamma$ non c’entra niente con il cammino $\Gamma$ tra i difetti, allora per tutti e quattro i collegamenti in $\gamma$ avremo $\tau = +1 $ e quindi in totale $W_\gamma = +1$. Consideriamo invece il caso in cui $\gamma$ è quadratino (placchetta) che racchiude uno tra $\widetilde{\boldsymbol{r}}$ e $\widetilde{\boldsymbol{r}}’$ (che appunto, in quanto siti del reticolo duale, sono al centro di quadratini del reticolo originale). In questo caso tre dei collegamenti in $\gamma$ hanno $\tau = +1$, mentre uno ha $\tau = -1$ e quindi in totale $W_\gamma = -1$. L’ultimo caso è quello in cui $\gamma$ è una placchetta che interseca $\Gamma$: in questo caso avremo due collegamenti con $+$ e due con $-$, per cui in totale $W_\gamma = +1$ di nuovo.
In una teoria di calibro, qualsiasi osservabile è esprimibile come combinazione di operatori di Wilson. Poiché come abbiamo visto l’operatore di Wilson non ha nessun interesse nel cammino $\Gamma$ ma è sensibile solo alle posizioni dei difetti, ne segue che la funzione di correlazione $\langle \mu(\widetilde{\boldsymbol{r}}) \mu(\widetilde{\boldsymbol{r}}’) \rangle$ è in realtà indipendente dal cammino $\Gamma$ utilizzato per definirla. Ne segue che i difetti $\mu$ apparentemente non-locali dalla definizione, sono in realtà operatori locali.
Si può dimostrare che i difetti sono collegati alla dualità di Kramers-Wannier, che abbiamo visto in un altro articolo. In particolare se $K = \beta J$ nel modello di Ising, abbiamo una trasformazione che ci porta ad un identico modello di Ising con $K \to K^* = -\frac12 \log\tanh K$. Kadanoff e Ceva hanno dimostrato che
$$\langle \sigma(\boldsymbol{r}) \sigma(\boldsymbol{r}’)\rangle_K = \langle \mu(\widetilde{\boldsymbol{r}}) \mu(\widetilde{\boldsymbol{r}}’) \rangle_{K^*}$$
Poiché $K\,\,\mathrm{grande} \leftrightarrow K^*\,\,\mathrm{piccolo}$ e viceversa, questa relazione conferma quella che abbiamo trovato nel precedente articolo.
