Consideriamo il modello di Ising in due dimensioni spaziali. Abbiamo degli spin classici $\sigma(\mathbf{r}) = \pm 1$ dove $\mathbf{r}$ indica il sito di un reticolo quadrato bidimensionale. L’Hamiltoniana contiene solo il termine d’interazione:
$$H = -J \sum_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} \sigma(\boldsymbol{r}) \sigma(\boldsymbol{r}’)$$
dove come al solito $\langle\boldsymbol{r}, \boldsymbol{r}’\rangle$ indica i primi vicini e $J > 0$ cosicché l’interazione è ferromagnetica.
Com’è noto, in due dimensioni il modello di Ising ha una transizione di fase. Per $T > T_c$ il sistema è in una fase disordinata, mentre per $T < T_c$ gli spin sono tutti allineati e la fase è ordinata. Questo comportamento è catturato da un parametro d’ordine, la magnetizzazione $m = \langle \sigma(\boldsymbol{r})\rangle$, che è nulla nella fase disordinata e non-nulla in quella ordinata:
$$\langle \sigma(\boldsymbol{r})\rangle = \begin{cases}
\neq 0 & T < T_c\,\,\mathrm{fase\,ordinata} \\
= 0 & T > T_c\,\,\mathrm{fase\,disordinata}
\end{cases}$$
Alternativamente, la fase ordinata/disordinata è individuata dal comportamento della funzione di correlazione,
$$\langle \sigma(\boldsymbol{r}) \sigma(\boldsymbol{r}’)\rangle \sim \begin{cases}
\mathrm{costante} & T < T_c\,\,\mathrm{fase\,ordinata} \\
\abs{\boldsymbol{r}-\boldsymbol{r}’}^{1/4} & T = T_c\,\,\mathrm{punto\,critico} \\
e^{-\abs{\boldsymbol{r}-\boldsymbol{r}’}/\xi} & T > T_c\,\,\mathrm{fase\,disordinata}
\end{cases}\tag{per $\abs{\boldsymbol{r}-\boldsymbol{r}’}$ grande}$$
Come abbiamo visto già in altri casi, questo secondo criterio per individuare le fasi risulta spesso più utile del precedente.
La cosa simpatica è che è possibile definire degli “operatori di disordine”. Ovvero è possibile definire delle variabili alternative con comportamento opposto alle $\sigma$: cioè che siano ordinate quando gli spin $\sigma$ sono disordinati, e viceversa.
La formulazione è dovuta a Kadanoff e Ceva, ma qui seguiamo Fradkin, Disorder Operators and their Descendants. Come sappiamo, ad ogni reticolo può essere associato un suo reticolo duale. Nel caso di un reticolo quadrato bidimensionale, il duale è un altro reticolo quadrato bidimensionale, solo un po’ spostato: i siti del reticolo duale sono i centri dei quadratini del reticolo originale, come nella figura:

Il reticolo originale (linea continua) e il reticolo duale (linea tratteggiata). I siti del reticolo duale (pallini neri) sono al centro dei quadratini del reticolo originale.
Ora definiamo la funzione di correlazione degli operatori di disordine. Per adesso non ci interessa quali siano gli operatori in sé, ma vediamo se riusciamo a riprodurre il comportamento che vogliamo. Come criterio per l’ordine/disordine prendiamo il comportamento della funzione di correlazione. Consideriamo quindi due siti $\widetilde{\boldsymbol{r}}, \widetilde{\boldsymbol{r}}’$ nel reticolo duale, e un cammino $\Gamma$ nel reticolo duale che li unisce. La situazione è esplicitata nell’immagine seguente:
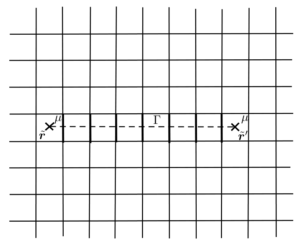
Il cammino $\Gamma$ nel reticolo duale (mostrato da una linea tratteggiata nell’immagine) intersecherà un certo numero di collegamenti del reticolo originale, mostrati in grassetto nella figura. Ora se $Z$ è la funzione di partizione del modello di Ising, chiamiamo $Z[\Gamma]$ la funzione di partizione dello stesso modello, dove però se $\Gamma$ interseca un collegamento $\langle\boldsymbol{r}, \boldsymbol{r}’\rangle$, allora per quella coppia di spin $J \to -J$, cioè l’accoppiamento diventa antiferromagnetico. In termini matematici,
$$Z = \sum_{\{\sigma\}} e^{-\beta H_\Gamma}$$
dove
$$H_\Gamma = -\sum_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} \sigma(\boldsymbol{r}) J_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} \sigma(\boldsymbol{r}’)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,J_{\langle\boldsymbol{r}, \boldsymbol{r}’\rangle} =
\begin{cases}
-J & \langle\boldsymbol{r}, \boldsymbol{r}’\rangle \in \Gamma \\
J & \mathrm{altrimenti}
\end{cases}
$$
Stiamo in altre parole introducendo una parete tra domini (“domain wall”) frazionaria, cioè spezzata. Questa è una specie di “difetto” nel cristallo.
La funzione di correlazione dei difetti è definita come
$$\langle \mu(\widetilde{\boldsymbol{r}}) \mu(\widetilde{\boldsymbol{r}}’) \rangle = \frac{Z[\Gamma]}{Z} \equiv e^{-\beta\Delta F[\Gamma]}$$
dove $\Delta F[\Gamma]$ può essere interpretata come l’eccesso di energia libera causato dalla presenza del difetto. La formula deriva dal fatto che $Z = e^{-\beta F}$. Qui abbiamo chiamato $\mu$ l’operatore di disordine che vive nel reticolo duale; non abbiamo definito cosa sia, né in realtà è ovvio che sia a priori definibile. Poi vedremo che lo è.
Per adesso ci accontentiamo di mostrare che la funzione di correlazione si comporta come vogliamo. Se $T \ll T_c$, cioè ben dentro la fase ordinata, tutti gli spin avranno la stessa direzione. Dando un’occhiata all’Hamiltoniana ci ricordiamo che due spin allineati contribuiscono $-J$ all’energia se non sono connessi da un punto della parete, quando invece contribuiscon $+J$. Poiché in questa fase sono tutti allineati o circa, la presenza di $\Gamma$ ci darà un contributo di $2J$ per ogni collegamento diventato antiferromagnetico. Questa è un’argomentazione un po’ euristica, ma ci dice che $\Delta F[\Gamma] \approx \kappa \abs{\widetilde{\boldsymbol{r}} -\widetilde{\boldsymbol{r}}’}$ per un qualche $\kappa > 0$. Pertanto la funzione di correlazione del disordine decade esponenzialmente. Al contrario, nella fase disordinata $T \gg T_c$, non c’è preferenza per $\pm$ tra i vari spin, e quindi l’intero difetto darà un contributo fisso indipendente dalla lunghezza. Pertanto la funzione di correlazione tenderà ad una costante. Abbiamo quindi:
$$\langle \mu(\widetilde{\boldsymbol{r}}) \mu(\widetilde{\boldsymbol{r}}’) \rangle \sim \begin{cases}
e^{-\kappa \abs{\widetilde{\boldsymbol{r}} -\widetilde{\boldsymbol{r}}’}}& T < T_c\,\,\mathrm{fase\,ordinata} \\
\abs{\widetilde{\boldsymbol{r}} -\widetilde{\boldsymbol{r}}’}^{-1/4} & T = T_c\,\,\mathrm{punto\,critico} \\
\mathrm{costante} & T > T_c\,\,\mathrm{fase\,disordinata}
\end{cases}\tag{per $\abs{\widetilde{\boldsymbol{r}} -\widetilde{\boldsymbol{r}}’}$ grande}$$
che è esattamente il comportamento opposto alla correlazione dei parametri d’ordine. In altre parole, ammesso che i “difetti” $\mu$ esistano indipendentemente (come vedremo), la fase ordinata dei $\sigma$ può anche essere vista come una fase disordinata dei difetti e viceversa la fase disordinata dei $\sigma$ corrisponde alla “condensazione dei difetti” che hanno un comportamento coerente.
Nel prossimo articolo continueremo la discussione dimostrando che in realtà $\langle \mu(\widetilde{\boldsymbol{r}}) \mu(\widetilde{\boldsymbol{r}}’) \rangle$ non dipende da quale cammino $\Gamma$ si sceglie, ma solo da $\widetilde{\boldsymbol{r}}$ e $\widetilde{\boldsymbol{r}}’$. Pertanto i $\mu$ sono delle unità indipendenti.
