Il primo scienziato a offrire la spiegazione corretta dell’arcobaleno è stato Cartesio. I raggi di luce del Sole vengono rifratti e riflessi all’interno delle gocce d’acqua sospese nell’aria, e concentrati in un punto particolare. In questo articolo seguiamo Berry, Nature’s optics and our understanding of light.
Consideriamo lo scenario della figura seguente:
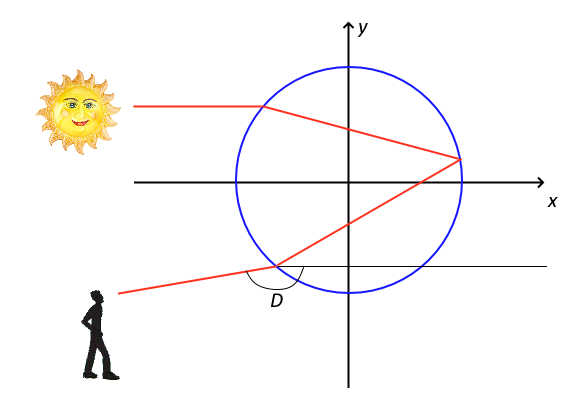
Il cerchio rappresenta la goccia d’acqua. Schematicamente, i raggi di luce solare viaggiano all’interno della goccia d’acqua, vengono concentrati in un punto specifico e poi raggiungono gli occhi dell’osservatore.
Approssimiamo la goccia d’acqua come una sfera con indice di rifrazione $n$, mentre l’indice di rifrazione dell’aria è $1$. Poniamo il raggio della sfera uguale ad $1$. Il sistema di riferimento che abbiamo disegnato è centrato nel cerchio della sfera e scelto in modo tale che il raggio di luce incidente (in rosso in alto a sinistra), proveniente dal Sole, sia parallelo all’asse $x$. Poiché il Sole è una sorgente molto lontana, tutti i raggi di luce saranno paralleli e distribuiti uniformemente in $y$, quindi possiamo immaginarli come una griglia fitta di rette costanti parallele a $x$ e quindi caratterizzate dal loro valore di $y$.
La situazione è illustrata con maggiore precisione nella figura seguente:

Il raggio di luce entra nella sferetta e viene rifratto una prima volta ($A$). Poi tocca l’altro lato della sferetta ($B$): una parte viene rifratta e fuoriesce (non disegnata), mentre una piccola parte viene riflessa verso l’altro lato della sfera. A questo punto il raggio viene rifratto una terza volta ($C$) e fuoriesce deviato di un angolo $D$. Quanto vale $D$?
Per risolvere il problema dobbiamo applicare la legge di Snell ad ogni rifrazione/riflessione. Nella prima rifrazione in $A$, l’angolo di incidenza dev’essere calcolato come al solito rispetto alla normale alla superficie, ed è pertanto semplicemente $\theta=\sin^{-1}(y)$. Ricordiamo che abbiamo posto il raggio della sfera uguale ad $1$, e quini $0 \leq y \leq 1$. Per la legge di Snell l’angolo di rifrazione $\theta’$ è quindi dato da
$$\sin\pqty{\sin^{-1}(y)} = n \sin{\theta’}\,\,\,\,\,\,\,\,\,\,\,\implies\,\,\,\,\,\,\,\,\,\,\,\theta’ = \sin^{-1}\pqty{\frac{y}{n}}$$
Ora passiamo al punto $B$. L’angolo di incidenza è di nuovo $\theta’$, perché il triangolo $AOB$ è isoscele, dato che due lati sono raggi della sfera. Poiché possiamo calcolare in questo caso $n \sin{\theta’} = y < 1$, non c’è riflessione totale. Quindi una buona parte del raggio di luce sarà rifratta e uscirà dalla goccia d’acqua: non ce ne curiamo. Una piccola parte, tuttavia, sarà riflessa e continuerà il viaggio dentro la goccia d’acqua. Nella figura è il raggio di luce da $B$ a $C$.
Poiché di nuovo $BOC$ è isoscele, l’angolo di incidenza in $C$ sarà di nuovo $\theta’$. Usando di nuovo la legge di Snell, l’ultima rifrazione dà quindi
$$n \sin \theta^{\prime} = \sin\theta^{\prime\prime}\,\,\,\,\,\,\,\,\,\,\,\implies\,\,\,\,\,\,\,\,\,\,\,\theta^{\prime\prime} = \sin^{-1}\pqty{y}$$
Rimane comunque da ottenere $D$. La differenza $D-\theta^{\prime\prime}$ è uguale all’angolo $\angle{EOC}$ in figura. Ma $\angle{EOC} =\angle{BOC} -\angle{BOE}$. Considerando il triangolo $BOC$ otteniamo che $\angle{BOC}=\pi-2\theta’$. Considerando invece il semicerchio superiore otteniamo $\theta + \angle{AOB} + \angle{BOE} = \pi$. Come prima possiamo calcolare $\angle{AOB}=\pi – 2\theta’$ e quindi mettendo tutto insieme il risultato finale è
$$D(y) = \pi -4\sin^{-1}\pqty{\frac{y}{n}}+2\sin^{-1}\pqty{y}$$
Il grafico di questa funzione per $0 \leq y \leq 1$ è dato nella figura seguente:
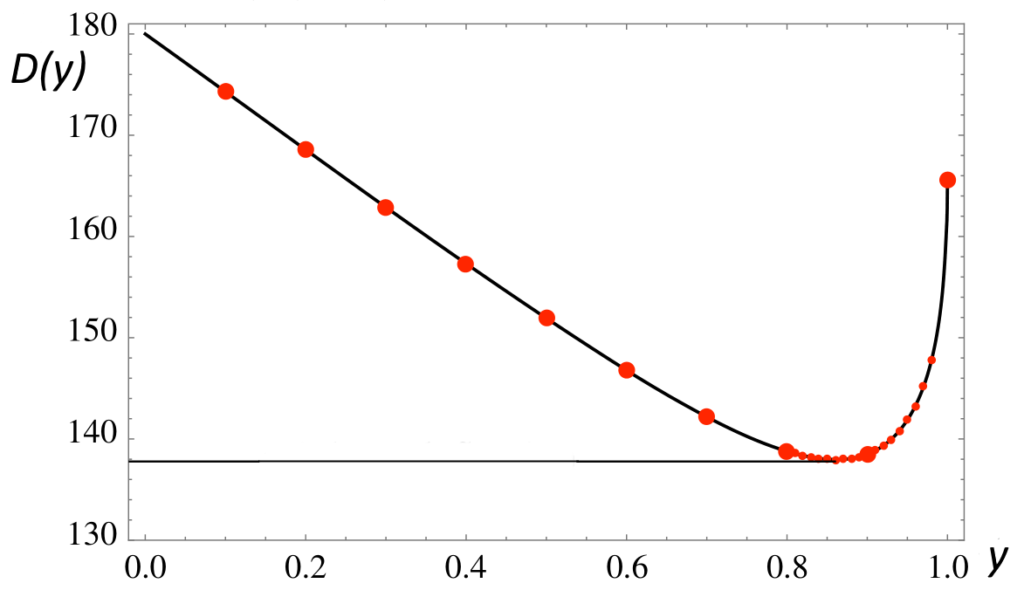
Adattata da Berry.
Possiamo calcolare esattamente la posizione del punto di minimo. Abbiamo
$$D'(y)=-\frac{4}{\sqrt{1-(y/n)^2}}+\frac{2}{\sqrt{1-y^2}}=0\,\,\,\,\,\,\,\,\,\,\,\implies\,\,\,\,\,\,\,\,\,\,\,y_{\mathrm{min}} = \sqrt{\frac{4-n^2}{3}}$$
Risostituendo e facendo uso di alcune identità trigonometriche, dopo un po’ di calcoli otteniamo
$$D(y_\mathrm{min}) = 2\cos^{-1}\pqty{ \frac{ \pqty{4-n^2}^{3/2}}{3 n^2 \sqrt{3}} }$$
L’indice di rifrazione dell’acqua è $n\approx 4/3$, per cui
$$D(y_\mathrm{min}) \approx 180^\circ -42^\circ$$
Il punto importante da notare è che sebbene i raggi di luce siano distribuiti uniformemente quando incidono sulla goccia, ne fuoriescono in maniera non-uniforme. In particolare, un gran numero di raggi sarà concentrato vicino al minimo di $D$. Questo perché vicino al minimo, $D$ è particolarmente piatta. Notiamo infatti dal grafico che tutti i punti da $y \approx 0,8$ a $y\approx 0,95$ danno come risultato $D \approx D(y_\mathrm{min}) \approx 180^\circ -42^\circ$. In altre parole un gran numero di raggi viene concentrato sulla deflessione minima: per cui in questo punto particolare della deflessione sarà visibile un fascio luminoso, che è appunto l’arcobaleno.
In particolare l’arcobaleno sarà quindi visibile per l’osservatore ad un angolo di $42^\circ$ rispetto alla direzione dei raggi solari. Geometricamente, fissando un angolo rispetto ad un osservatore descriviamo un cono, e questo spiega perché l’arcobaleno è curvo: l’osservatore vede un arcobaleno ovunque i suoi occhi formino un angolo di $42^\circ$ rispetto alla direzione dei raggi del Sole.
L’ultimo effetto da considerare sono i colori. Poiché la luce di diversi colori ha diversi indici di rifrazione, l’angolo di deflessione minimo dipende debolmente dalla lunghezza d’onda della luce considerata. La luce solare è bianca, cioè contiene circa tutte le lunghezze d’onda; passando dentro la goccia d’acqua i raggi di diverse lunghezze d’onda vengono rifratti in maniera diversa, formando così le bande colorate dell’arcobaleno.
Una simile spiegazione si applica anche per altri fenomeni collegati, come ad esempio gli arcobaleni doppi.
