La valutazione dell’accuratezza di un test per una malattia si base su alcune idee non banali di teoria della probabilità. In questo articolo vediamo il significato di vari termini come sensibilità e specificità, falso positivo e falso negativo, e vedremo in quali condizioni uno o l’altro caso è prevalente. Per chi vuole solo un semplice esempio pratico, lo trovate alla fine.
La probabilità condizionata e il teorema di Bayes
Indichiamo con $p(A)$ la probabilità che avvenga $A$. Quindi ad esempio usando la notazione insiemistica indichiamo con $p(A \cap B)$ la probabilità che avvengano sia $A$ che $B$. La probabilità condizionata è la probabilità che avvenga un certo evento $A$ sapendo che $B$ è avvenuto, e la indichiamo con $p(A | B)$.
Per chiarire la situazione guardiamo l’immagine seguente:
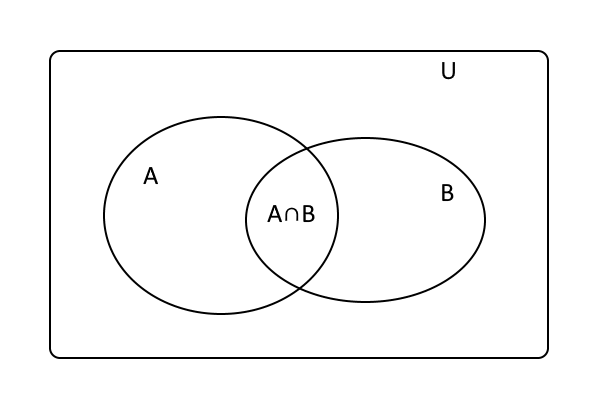
Abbiamo i due eventi, $A$ e $B$, che si intersecano in maniera non banale. Se non avessero intersezione, allora $A$ e $B$ non potrebbero avvenire insieme e quindi la loro probabilità condizionata sarebbe nulla. $U$ è l’insieme universo. Ora chiamiamo $N(A)$ il numero di elementi dell’insieme $A$ e soltanto $N$ il numero di elementi totali. Allora abbiamo per definizione $p(A) = N(A)/N$. Dalla definizione di probabilità condizionata sappiamo che $B$ è già avvenuto, per cui nel calcolare $p(A | B)$ dobbiamo restringere l’insieme totale al solo $B$. In altre parole, dobbiamo chiederci: tra gli eventi in $B$, quanti sono anche eventi di $A$? La probabilità è perciò data da
$$p(A | B) = \frac{N(A \cap B)}{N(B)}=\frac{N(A \cap B)}{N}\frac{N}{N(B)}=\frac{p(A \cap B)}{p(B)}$$
Ora possiamo effettuare lo stesso calcolo scambiando $A$ e $B$, ottenendo $p(B|A) = p(B \cap A) / p(A)$ e quindi poichè $p(A \cap B) = p(B \cap A)$ otteniamo il cosiddetto teorema di Bayes,
$$\boxed{p(A | B) = \frac{p(A)}{p(B)} p(B | A)}$$
Questa è una formula quantitativa che permette di mettere in relazione le due probabilità condizionate $p(A | B)$ e $p(B | A)$, ma soprattutto ci dice che le due probabilità condizionate possono essere molto diverse tra loro. Nel prossimo paragrafo vediamo un esempio pratico.
Falsi negativi e positivi, sensibilità e specificità
Supponiamo di fare un test antigenico per il coronavirus. In questo caso abbiamo diverse probabilità condizionate da considerare, tra cui
- La probabilità che il test sia positivo sapendo che la persona è positiva $p(\mathrm{test}\,+|\mathrm{persona}\,+)$. Questa probabilità viene definita la sensibilità del test.
- La probabilità che il test sia negativo sapendo che la persona è negativa $p(\mathrm{test}\,-|\mathrm{persona}\,-)$. Questa è la specificità del test.
In altre parole la sensibilità del test è una misura di quanto il test sia in grado di identificare correttamente le persone positive, mentre la specificità ci dice quanto il test è in grado di identificare correttamente le persone negative. La teoria della probabilità ci dice prima di tutto che questi due valori possono essere anche molto diversi tra loro e comunque non c’è motivo per cui debbano essere uguali. Queste due quantità sono quelle riportate dal produttore, che può misurarle sperimentalmente. Ad esempio se si vuole calcolare la specificità e la sensibilità di un test antigenico, si può effettuare sia il test antigenico sia un test PCR ad un gran numero di persone e misurare le due probabilità supponendo che il test PCR sia sempre corretto (il che non è strettamente vero ma è una buona approssimazione).
In ogni caso a noi utenti dei test non interessa sapere direttamente la sensibilità o la specificità del test, perchè queste sono probabilità calcolate con l’assunto che la persona è positiva o negativa. Al contrario a noi viene dato il risultato del test, positivo o negativo, e vorremmo sapere qual’è la probabilità che il risultato del test sia corretto. Ciò corrisponde a diverse probabilità condizionate:
- La probabilità che la persona è negativa sapendo che il test ha dato risultato positivo $p(\mathrm{persona}\,-|\mathrm{test}\,+)$. Questa situazione corrisponde ad un falso positivo.
- La probabilità che la persona è positiva sapendo che il test ha dato risultato negativo $p(\mathrm{persona}\,+|\mathrm{test}\,-)$. In questo caso abbiamo un falso negativo.
Ovvero il “falso” positivo o negativo avviene quando il risultato è sbagliato, una volta noto il risultato del test. Chiaramente possiamo anche avere le probabilità condizionate di un vero positivo e di un vero negativo, quando il risultato del test è corretto.
Il teorema di Bayes ci permette di stabilire la relazione tra falsi negativi e falsi positivi e le due misure fornite dal produttore, cioè la sensibilità e la specificità. Ad esempio abbiamo
\begin{align}
p(\mathrm{persona}\,+ | \mathrm{test}\,-) &= \frac{p(\mathrm{persona}\,+)}{p(\mathrm{test}\,-)} p(\mathrm{test}\,- | \mathrm{persona}\,+)=\\
&=\frac{p(\mathrm{persona}\,+)}{p(\mathrm{test}\,-)} \bqty{1-p(\mathrm{test}\,+ | \mathrm{persona}\,+)}
\end{align}
Ovvero il tasso di falsi negativi $p(\mathrm{persona}\,+ | \mathrm{test}\,-)$ dipende dalla sensibilità del test $p(\mathrm{test}\,+ | \mathrm{persona}\,+)$, ma anche dall’incidenza del virus nella popolazione $p(\mathrm{persona}\,+)$ in rapporto alla proporzione di test negativi $p(\mathrm{test}\,-)$. Perciò l’affidabilità del test dipende anche dalla situazione epidemiologica. Volendo fare una stima del tasso di falsi negativi per un test antigenico, ne conosciamo la sensibilità e possiamo trovare i dati sulla percentuale di test negativi. In linea di principio non siamo in grado di conoscere $p(\mathrm{persona}\,+)$ perchè non siamo a disposizione di un test perfetto per la malattia. Potremmo stimarlo usando il tasso di positività dei test PCR, che sono molto affidabili, ma sorge un problema, perché la popolazione che si sottopone ad un test PCR non è in linea di principio la stessa che si sottopone ad un test antigenico (potrebbe avere ad esempio sintomi più gravi).
Un semplice esempio
In quest’ultima sezione vediamo un semplice esempio concreto. Abbiamo visto che la percentuale di falsi positivi e negativi dipende anche dalla situazione epidemiologica, cioè dall’incidenza nel virus nella popolazione. Qui mostreremo che
- Se l’incidenza del virus è bassa, cioè ci sono pochi casi, allora c’è principalmente il rischio di falsi positivi.
- Se l’incidenza del virus è alta, cioè ci sono molti casi, allora c’è principalmente il rischio di falsi negativi.
Supponiamo che il test antigenico abbia sia una sensibilità che una specificità del $90\%$. Ora supponiamo che l’incidenza del virus sia relativamente bassa, cioè mettiamo che la prevalenza del virus nella popolazione sia del $20\%$. Supponiamo che $100$ persone a caso si sottopongano al test. Di queste $100$ persone, $20$ avranno il virus e $80$ no. Poichè il test ha una sensibilità del $90\%$, tra le $20$ persone positive $18$ saranno correttamente identificate come positive (vere positive), mentre invece $2$ saranno identificate erroneamente come negative (false negative). Tra le $80$ che non hanno il virus, poichè la specificità è anch’essa del $90\%$, allora $72$ saranno correttamente identificate come negative (vere negative), mentre $8$ saranno identificate erroneamente come positive (false positive). Da questa analisi vediamo che in totale avremo $26$ test positivi e $74$ test negativi. Tra questi, $8$ su $26$, cioè circa il $30\%$ dei positivi sono falsi positivi, mentre solo $2$ su $76$ negativi sono falsi negativi, cioè solo circa l’$1,3\%$.
Ripetendo il calcolo nel caso in cui l’incidenza nella popolazione è alta, mettiamo l’$80\%$, otterremmo il risultato opposto in cui il $30\%$ dei test negativi è falso negativo, mentre i falsi positivi sono ben pochi.
I test nel mondo reale
Come mostrato nel documento di riepilogo dell’Unione Europea, la maggior parte dei test antigenici approvati nell’Unione ha una sensibilità di $\approx 95\%$ e una specificità di circa il $\approx 99\%$. In realtà online si trovano anche diversi articoli di ricerca secondo cui la specificità sarebbe si’ del $99\%$, ma la sensibilità circa $\approx 80\%$. Non so a cosa sia dovuta questa discrepanza.
In ogni caso il Covid ha un’incidenza in realtà molto bassa, che non supera l’$1\%$ della popolazione. Perciò nonostante la sensibilità sia più bassa della specificità, il rischio principale è quello di falsi positivi, che si verifica in maniera molto più probabile nei periodi di bassissima incidenza, come ad esempio nell’estate 2020.
