Consideriamo il modello di Ising classico in due dimensioni, dato dall’Hamiltoniana
$$H = -J \sum_{\langle ij \rangle} s_{i} s_{j}$$
dove $i$ e $j$ sono i siti di un reticolo quadrato bidimensionale, $\langle ij \rangle$ indica primi vicini, $s_i = \pm 1$ e $J > 0$. La funzione di partizione del modello è data da
$$Z(\beta) = \sum_{\{s\}} e^{-\beta H}$$
dove la somma è su tutte le possibili configurazioni degli spin. Poiché $\beta$ e $J$ appaiono nel modello solo tramite il loro prodotto $\beta J$, possiamo porre $J=1$ senza perdita di generalità. La dualità di Kramers-Wannier è una simmetria del modello che permette di mettere in relazione il valore della funzione di partizione a temperature diverse. Vediamo come funziona.
La trasformazione
Partiamo dalla funzione di partizione del modello, che scriviamo nel modo seguente:
$$Z(\beta) = \sum_{\{s\}} e^{-\beta H} = \sum_{\{s\}}\prod_{\langle ij \rangle} e^{\beta s_i s_j}$$
Possiamo inoltre scrivere l’esponenziale in termini del seno e del coseno iperbolico. Infatti $e^{x} = \cosh{x}+\sinh{x}$. Poiché $s_i = \pm 1$, allora anche $s_i s_j = \pm 1$ e quindi utilizzando la (dis)parità del seno e del coseno iperbolico, abbiamo
$$e^{\beta s_i s_j} = \cosh{\beta}+s_i s_j\sinh{\beta}$$
Ora definiamo
$$f_k(\beta) = \begin{cases}\cosh{\beta} & k = 0\\ \sinh{\beta} & k = 1\end{cases}$$
e quindi in questi termini
$$e^{\beta s_i s_j} = \sum_{k=0}^1 f_k(\beta)(s_i s_j)^k$$
Quindi tornando alla funzione di partizione,
$$Z(\beta) = \sum_{\{s\}}\prod_{\langle ij \rangle} \sum_{k=0}^1 f_k(\beta)(s_i s_j)^k$$
Ora possiamo invertire la somma su $k$ e il prodotto sulle coppie $\langle i j\rangle$ in maniera simile a quanto abbiamo già fatto in passato, ad esempio qui. Abbiamo
$$Z(\beta) = \sum_{\{s\}}\sum_{\{k\}}\prod_{\langle ij \rangle} f_{k_{\langle ij \rangle}}(\beta)(s_i s_j)^{k_{\langle ij \rangle}}$$
In questo senso, ad ogni coppia $\langle ij \rangle$ di primi vicini assegniamo un $k_{\langle ij \rangle} = 0,1$; la sommatoria $\{k\}$ è quindi su tutte le tali possibili configurazioni dei $k$. Adesso spezziamo l’ultima produttoria in due parti:
$$\prod_{\langle ij \rangle} f_{k_{\langle ij \rangle}}(\beta)(s_i s_j)^{k_{\langle ij \rangle}}=\pqty{\prod_{\langle ij \rangle} f_{k_{\langle ij \rangle}}(\beta) }\pqty{\prod_{\langle ij \rangle} (s_i)^{k_{\langle ij \rangle}} (s_j)^{k_{\langle ij \rangle}}}$$
Vogliamo trasformare la seconda produttoria in una produttoria sui siti $i$ invece che sulle coppie $\langle ij \rangle$ di primi vicini. Abbiamo
$$\prod_{\langle ij \rangle} (s_i)^{k_{\langle ij \rangle}} (s_j)^{k_{\langle ij \rangle}} =\prod_{i} (s_i)^{\sum_{\langle ij \rangle} k_{\langle ij \rangle}}$$
La sommatoria nell’esponente va considerata come la sommatoria su tutti i $j$ tali che $i$ e $j$ siano primi vicini. Infatti nel prodotto sui primi vicini $\langle ij \rangle$ ogni sito $i$ appare esattamente quattro volte, poiché siamo su un reticolo rettangolare in due dimensioni. Ogni sito $i$ ha quattro primi vicini, e ognuna di queste quattro coppie di primi vicini apparirà una sola volta nella produttoria. Otteniamo quindi:
$$Z(\beta) = \sum_{\{s\}}\sum_{\{k\}}\pqty{\prod_{\langle ij \rangle} f_{k_{\langle ij \rangle}}(\beta) } \prod_{i} (s_i)^{\sum_{\langle ij \rangle} k_{\langle ij \rangle}}$$
Ora solo l’ultimo termine dipende da $s$, per cui possiamo spostare la somma su $\{s\}$ alla fine e invertirla con la produttoria, in maniera analoga a quanto fatto prima per $k$:
$$Z(\beta) = \sum_{\{k\}}\pqty{\prod_{\langle ij \rangle} f_{k_{\langle ij \rangle}}(\beta) } \prod_{i} \sum_{s=\pm 1} s^{\sum_{\langle ij \rangle} k_{\langle ij \rangle}}$$
Ora consideriamo $\sum_{s=\pm 1} s^n = 1 +(-1)^n$. Questa è uguale a $0$ se $n$ è dispari, mentre è uguale a $2$ se $n$ è pari. Scriviamo quindi $\sum_{s=\pm 1} s^n = 2\delta_2(n)$, dove $\delta_2$ è una funzione delta “$\mathrm{mod}\,2$”: vale $1$ nel caso $n$ è pari (cioè $n \equiv 0\,\,(\mathrm{mod}\,2)$) e vale $0$ altrimenti. Pertanto
$$Z(\beta) = \sum_{\{k\}}\pqty{\prod_{\langle ij \rangle} f_{k_{\langle ij \rangle}}(\beta) } \prod_{i} 2\delta_2\pqty{{\sum_{\langle ij \rangle} k_{\langle ij \rangle}}}$$
In pratica le uniche configurazioni che contano sono quelle per cui la somma dei $k$ in ogni sito sia pari. Questo vincolo ci permette di scrivere i $k$ in una maniera molto semplice. Per farlo ci serve il concetto di reticolo duale, che è molto in uso ad esempio in materia condensata:
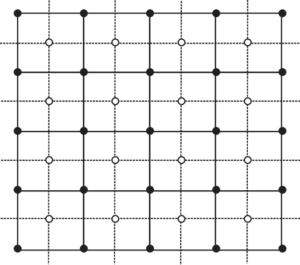
Reticolo e reticolo duale
L’immagine mostra il reticolo rettangolare originale con la lina continua e i siti in nero; il reticolo duale in questo caso è di nuovo un reticolo rettangolare, ed è mostrato con la linea tratteggiata e i siti in bianco. In pratica è il reticolo i cui siti si trovano al centro dei quadratini formati dai siti del reticolo originale.
Nel nostro caso i $k$ vivono nelle connessioni tra due siti primi vicini nel reticolo originale. Ognuna di queste connessioni interseca esattamente una connessione tra due siti primi vicini nel reticolo duale. Data una connessione $\langle ij \rangle$ tra due siti $i$ e $j$ del reticolo originale, chiamiamo la connessione duale $\widetilde{\langle ij \rangle}$, ovvero $\widetilde{\langle ij \rangle}$ è l’unica connessione del reticolo duale che interseca la connessione $\langle ij \rangle$ del reticolo originale. Poniamo poi per convenzione $\widetilde{\langle ij \rangle}=\langle \widetilde{i}\widetilde{j} \rangle$. Ovvero definiamo i siti $\widetilde{i}$ e $\widetilde{j}$ del reticolo duale come i siti primi vicini connessi da $\widetilde{\langle ij \rangle}$. La situazione è riassunta nell’immagine seguente:
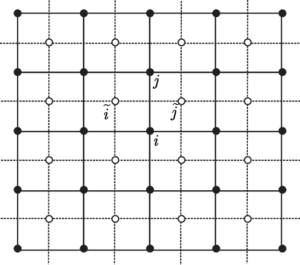
Connessioni e connessioni duali
Per risolvere completamente il vincolo della funzione delta definiamo delle nuove variabili $\sigma_{\widetilde{i}}=\pm 1$ su ogni sito $\widetilde{i}$ del reticolo duale e quindi poniamo
$$k_{\langle ij \rangle} = \frac{1}{2}\pqty{1-\sigma_{\widetilde{i}}\sigma_{\widetilde{j}}}$$
in modo che correttamente $k_{\langle ij \rangle} = 0, 1$. Con questa definizione,
$$\sum_{\langle ij \rangle} k_{\langle ij \rangle} = 2-\frac{1}{2}\pqty{\sigma_1 \sigma_2 + \sigma_2 \sigma_3 + \sigma_3 \sigma_4 + \sigma_4 \sigma_1}$$
dove $\sigma_1, \sigma_2, \sigma_3, \sigma_4$ sono come nell’immagine seguente:
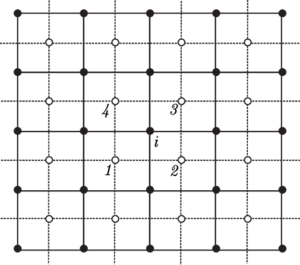
Possiamo controllare manualmente che per ogni possibile scelta di $\sigma_{\widetilde{i}}=\pm 1$ la somma è pari. Ciò dimostra che questa scelta per i $k$ è sufficiente a risolvere il vincolo. È anche possibile dimostrare che questa scelta è necessaria.
Sostituendo nella funzione di partizione le funzioni delta sono soddisfatte automaticamente per costruzione, e quindi otteniamo:
$$Z(\beta) =2^N \frac{1}{2} \sum_{\{\sigma\}}\pqty{\prod_{\langle \widetilde{i}\widetilde{j} \rangle} f_{\frac{1}{2}\pqty{1-\sigma_{\widetilde{i}}\sigma_{\widetilde{j}}}}(\beta) }$$
dove $N$ è il numero di siti del reticolo e il fattore $2^N$ viene dal fattore davanti alla funzione delta. Stavolta la somma è sulle configurazioni dei $\sigma$ e il prodotto è sui primi vicini nel reticolo duale. Il fattore di $1/2$ è dovuto al fatto che scambiando $\sigma \to -\sigma$ otteniamo gli stessi $k$; per cui sommando sui $\sigma$ invece che sui $k$ stiamo contando le configurazioni due volte.
Ora vogliamo riscrivere $f_k(\beta)$ di nuovo come un’esponenziale. Poiché $k=0,1$ possiamo scrivere $f_k(\beta) = \cosh(\beta) (\tanh(\beta))^k$ in modo da ottenere coseno e seno iperbolici nei due casi. In termini di esponenziali abbiamo quindi $f_k(\beta) = \cosh(\beta) \exp{\bqty{k\log\tanh(\beta)}}$ e quindi sostituendo
$$Z(\beta) =2^N \frac{1}{2} \sum_{\{\sigma\}}\prod_{\langle \widetilde{i}\widetilde{j} \rangle} \pqty{\cosh{\beta} \sinh{\beta}}^{1/2} e^{-\frac{1}{2}\sigma_{\widetilde{i}}\sigma_{\widetilde{j}}\log\tanh(\beta) }=\\
=\pqty{2\cosh{\beta} \sinh{\beta}}^N \frac{1}{2} \sum_{\{\sigma\}} \exp{\pqty{-\frac{1}{2} \log\tanh(\beta) \sum_{\langle \widetilde{i}\widetilde{j} \rangle}\sigma_{\widetilde{i}}\sigma_{\widetilde{j}} }}$$
Quest’ultima è di nuovo la funzione di partizione di un modello di Ising, stavolta però sul reticolo duale con le variabili $\sigma$ e invece di $\beta$ abbiamo $-\frac{1}{2} \log\tanh(\beta)$. In altre parole ponendo $\beta^* = -\frac{1}{2} \log\tanh(\beta)$ abbiamo
$$Z(\beta) = \frac{\pqty{\sinh{(2\beta)}}^N}{2} Z(\beta^*)$$
Ovvero, a meno di una costante, la funzione di partizione è invariante rispetto alla trasformazione $\beta \to \beta^*$. Notiamo inoltre che $\beta^*$ ha un comportamento inverso rispetto a $\beta$: è piccolo per $\beta$ grande e grande per $\beta$ piccolo. Cioè la dualità di Kramers-Wannier scambia tra di loro le due fasi ad alta e bassa temperatura.
Dato che siamo in grado ad esempio di effettuare uno studio del modello tramite la teoria delle perturbazioni per $\beta$ piccolo, il fatto che la dualità scambia le due fasi è estremamente utile: in questa maniera possiamo utilizzare la teoria delle perturbazioni anche per $\beta$ grande, scambiando $\beta \to \beta^*$, e applicandola a $\beta^*$ che è piccolo.
Il fatto che alla fine di questa procedura si ha di nuovo un modello di Ising non è affatto scontato: si dice perciò che Ising in due dimensioni è auto-duale. La dualità può essere applicata in qualsiasi dimensione e anche in altri modelli, ed è spesso estremamente utile, ma solo raramente i modelli sono auto-duali.
L’energia libera e la transizione di fase
Un ultimo utilizzo della dualità è che permette di ottenere il valore esatto della temperatura critica della transizione di fase nel modello di Ising 2D. Infatti l’energia libera è data da
$$F(\beta) = \lim_{N \to \infty} -\frac{1}{\beta N} \log{Z(\beta)}$$
Utilizzando la relazione di dualità per le funzioni di partizione otteniamo:
$$F(\beta) = -\frac{1}{\beta } \log{\sinh(2\beta)}+F(\beta^*)$$
La transizione di fase avviene in un punto di non-analiticità di $F$. Poiché il termine centrale è analitico per ogni $\beta > 0$, se $\beta_c$ è un punto critico, allora anche $\beta_c^*$ dev’essere un punto critico. Poiché in questo caso il punto critico è unico, dobbiamo necessariamente avere $\beta_c^* = \beta_c$, la cui unica soluzione è data da
$$\beta_c = \frac{1}{2}\log{\pqty{1+\sqrt{2}}}$$
che è il valore esatto del punto critico.
La dualità ci ha permesso di individuare il punto della transizione di fase perché già sappiamo che esiste una sola transizione al variare di $\beta$. Se il modello avesse avuto più di un punto critico avremmo invece ottenuto delle relazioni tra coppie di punti critici.
