Abbiamo visto in un precedente articolo il modello SIS in epidemiologia, che si applica alle malattie che non producono immunità e che hanno una letalità trascurabile. Il modello SIR si applica alle malattie che producono immunità nei soggetti che guariscono. Inoltre terremo anche conto del fatto che la malattia può avere una letalità non nulla, cioè la malattia può uccidere una certa parte degli individui che la contraggono.
In questo caso abbiamo tre categorie di persone: come prima i suscettibili $S$ e gli infetti $I$, e ora aggiungiamo anche i guariti $R$ (dall’inglese “recovered”). Tutta la popolazione $N$ è divisa in questi tre gruppi, quindi $S+I+R=N$.
La dinamica nella popolazione è mostrata nella figura sotto. Una persona suscettibile può solo contrarre la malattia e diventare infetta, $S \to I$; una persona infetta può guarire dalla malattia e diventare immune, quindi $I \to R$.
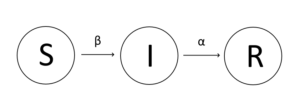
Questo modello può includere anche le morti causate dalla malattia. Per fare ciò basta includere in $R$ anche i morti: dal punto di vista della malattia, una persona morta è equivalente ad una persona guarita: entrambe non possono contrarre la malattia, né trasmetterla. In tal caso $\alpha$ non è più solo il tasso di guarigione, ma la somma del tasso di guarigione e del tasso di mortalità. In ogni caso per semplificare chiameremo $\alpha$ il tasso di guarigione e tutte le persone in $R$ come guarite.
La formulazione matematica è molto simile a quella del modello SIS. Il numero di persone guarite in ogni istante di tempo è un tasso fisso rispetto al numero di infetti; il numero di persone contagiate ad ogni istante di tempo è invece proporzionale sia ad $S$ che ad $I$, per cui:
$$S'(t) = -\beta S I\\
I'(t) = \beta S I -\alpha I\\
R'(t) = \alpha I$$ In totale abbiamo $S'(t) + I'(t) + R'(t)=0$ per cui il numero totale di persone della popolazione è costante, $S+I+R = N$.
Una prima cosa da notare in questo modello è che $S'(t) < 0$, per cui il numero di suscettibili decresce sempre. Questo non vuol dire che diventerà necessariamente zero, ma potrebbe terminare in un asintoto. Al contrario $R'(t) > 0$, per cui il numero di guariti aumenta sempre. Queste due caratteristiche non sono davvero sorprendenti, perché seguono in maniera diretta dal modo in cui abbiamo costruito il modello: non c’è maniera per un individuo di entrare in $S$, ma solo di uscirne; alla stessa maniera, non c’è modo di uscire da $R$.
Possiamo dimostrare che:
- $S(t) \to S_{\infty} > 0$ per $t \to \infty$, cioè c’è sempre una percentuale della popolazione che non viene toccata dalla malattia.
- $I(t) \to 0$ per $t \to \infty$, cioè la malattia sparisce sempre e non diventa mai endemica.
Dal modello notiamo che $R$ non entra mai nei membri destri dell’equazione, quindi possiamo ignorarlo e ricavarlo da $R = N-S-I$. Vediamo di dimostrare queste affermazioni
Dividendo la prima equazione per la terza otteniamo
$$\dv{S}{R} = -\frac{\beta}{\alpha} S $$
Per cui abbiamo $S = S(0) e^{-\beta R /\alpha}$. Poiché $R \leq N$, allora
$$S = S(0) e^{-\beta R /\alpha} \geq S(0) e^{-\beta N /\alpha} > 0$$
per cui $S$ non può mai essere nulla, e quindi $S \to S_{\infty}>0$ per $t \to \infty$.
Per dimostrare la seconda affermazione, integriamo tra $0$ e $\infty$ la prima equazione, ottenendo:
$$S_\infty – S_0 = -\beta \int_0^\infty S(t) I(t)$$
Poiché $S$ è decrescente, abbiamo anche $S > S_{\infty}$, per cui
$$S_0 – S_\infty = \beta \int_0^\infty S(t) I(t) \geq \beta S_\infty \int_0^\infty I(t)$$
Poiché $I$ è positiva e il suo integrale è limitato, allora $I(t) \to 0$. Infatti se $I(t)$ tendesse ad un asintoto o non tendesse a zero, l’integrale sarebbe infinito.
Picco di contagi
Simulando numericamente le equazioni sopra si ottengono delle traiettorie diverse per il numero di contagiati $I$ in base a diverse scelte di condizioni iniziali, come mostrato nella figura sotto:
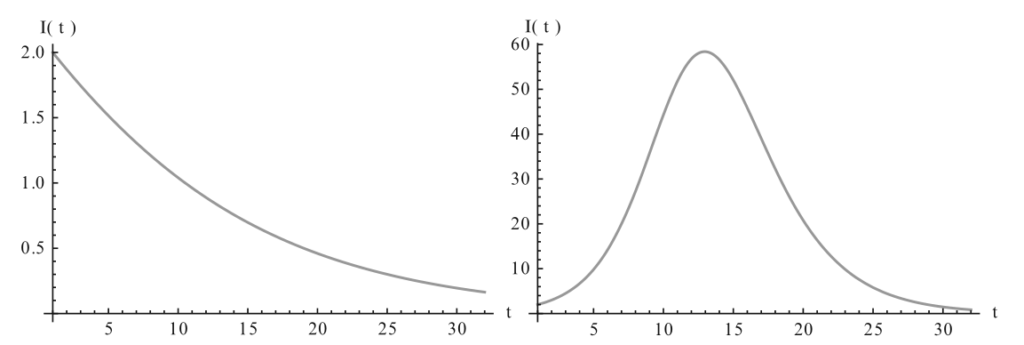
Evoluzione del modello SIR con diverse situazioni di partenza. Presa da Martcheva, An Introduction to Mathematical Epidemiology
Per cui il numero di infetti può decrescere monotonicamente, oppure può aumentare e poi decrescere. Diventa quindi di interesse individuare il picco di contagi, cioè il massimo di $I$. Dividendo la seconda equazione per la prima otteniamo:
$$\dv{I}{S} = -1 + \frac{\alpha}{\beta S}$$
Integrando otteniamo,
$$I = -S +\frac{\alpha}{\beta} \log{S} + C$$
$$C = $$
La costante $C$ può essere determinata calcolando il limite per $t \to \infty$, in cui sappiamo che $S \to S_\infty>0$ e $I \to 0$. Pertanto abbiamo
$$I = -(S-S_\infty) +\frac{\alpha}{\beta} \log{\frac{S}{S_\infty}}$$
Possiamo quindi inserire anche le condizioni iniziali $(I_0, S_0)$ e così facendo otteniamo una equazione tra $\alpha/\beta, S_0, I_0, S_\infty$, che può essere utilizzata per stimare uno qualsiasi dei suoi termini.
Il picco dei contagi è raggiunto quando $I'(t)=0$, cioè, utilizzando la seconda equazione, quando
$$S=\frac{\alpha}{\beta}$$
Sostituendo nella relazione tra $S$ e $I$, abbiamo
$$I_{\mathrm{max}} = -\pqty{\frac{\alpha}{\beta}-S_\infty}+\frac{\alpha}{\beta} \log{\frac{\alpha}{\beta S_\infty}}$$
Oppure se preferiamo possiamo utilizzare una delle formule precedenti per rimpiazzare $S_\infty$ con $S_0$ e $I_0$ in maniera appropriata.
A differenza che nei modelli SIS, in questo caso non abbiamo situazioni di equilibrio vero e proprio.
