Per capire come funziona in linea di principio il meccanismo di Higgs, ovvero la cosiddetta “rottura spontanea di una simmetria di calibro” (gauge), studieremo un modello semplificato che consente di vedere l’essenza della questione: l’elettrodinamica scalare, ovvero una teoria di calibro $\mathrm{U}(1)$ accoppiata ad un campo scalare.
Da un punto di vista fisico il meccanismo di Higgs spiega l’osservazione sperimentale di bosoni vettori ($A_\mu$) massivi senza rompere la simmetria di calibro. Includere banalmente un termine di massa per $A_\mu$, cioè una roba tipo $m^2 A_\mu A^\mu$ rompe infatti la simmetria di calibro in modo esplicito.
Il meccanismo di Higgs viene chiamato “rottura spontanea di una simmetria di calibro”. Tuttavia, una simmetria di calibro non può essere rotta. Ciò segue semplicemente dall’osservazione che la simmetria di calibro non è una vera simmetria, ma solo una “ridondanza” nella nostra descrizione della natura: due configurazioni collegate da una simmetria di calibro sono a tutti gli effetti la stessa configurazione. Ciò non è vero per una simmetria globale: ad esempio, un vettore ruotato è diverso dal vettore originale, ma se l’energia è rotazionalmente invariante le due configurazioni, pur diverse, hanno la stessa energia. Scegliere uno dei due vettori rompe la simmetria perché i vettori sono diversi. Due configurazioni collegate da una trasformazione di calibro sono invece fisicamente la stessa configurazione e strettamente parlando la simmetria di calibro non è mai rotta.
In termini più precisi, il teorema di Elitzur dimostra che in una teoria quantistica di calibro, gli unici operatori che possono avere un valore atteso non-nullo nel vuoto sono invarianti di calibro. Ovvero se $O$ non è invariante di calibro, allora necessariamente $\langle O \rangle=0$. Di nuovo, ciò dimostra che è impossibile rompere spontaneamente la simmetria di calibro. Vediamo allora cosa si intende per “rottura spontanea di una simmetria di calibro”.
Il potenziale a cappello messicano
La Lagrangiana della teoria è data da:
$$\mathcal{L} = -\frac{1}{4} F_{\mu\nu} F^{\mu\nu} + \pqty{D^\mu \phi}^* \pqty{D_\mu \phi} -V\pqty{\phi^* \phi}\tag{1}$$
dove $\phi$ è un campo scalare complesso, $A_\mu$ è il campo di calibro, $F_{\mu\nu} = \partial_\mu A_\nu -\partial_\nu A_\mu$ è il tensore elettromagnetico. La derivata covariante $D_\mu = \partial_\mu -i e A_\mu$ serve a far sì che il termine cinetico sia invariante rispetto alle trasformazioni di calibro,
$$\phi(x) \to e^{i e \alpha(x)} \phi(x) \,\,\,\,\,\,\,\,\,\,\, A_\mu \to A_\mu + \partial_\mu \alpha$$
Il potenziale $V$ causa la “rottura spontanea di simmetria”. Includiamo tutti i termini rinormalizzabili:
$$V\pqty{\phi^* \phi} = \mu \phi^* \phi + \lambda \pqty{\phi^* \phi}^2\tag{2}$$
Il potenziale ha le due seguenti possibili forme:
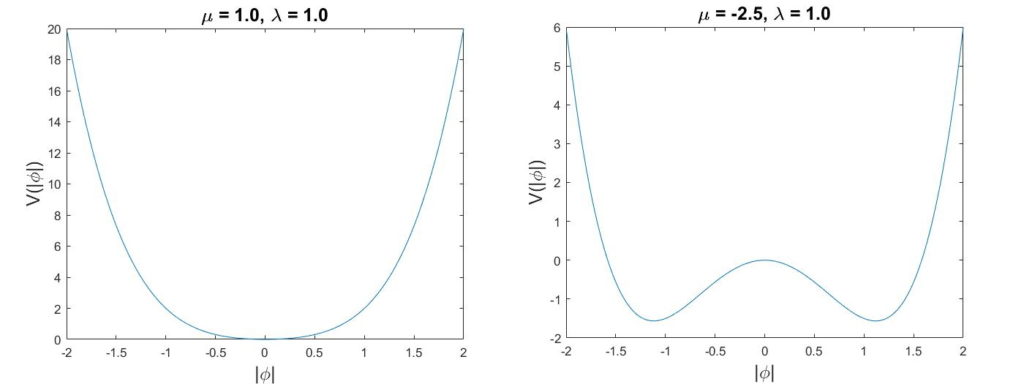
Per $\mu > 0$, come nella prima immagine, il potenziale ha un unico minimo in $\abs{\phi}=0$. Invece per $\mu < 0$, come nella seconda immagine, abbiamo un minimo per $\abs{\phi}\neq 0$. Nell’immagine abbiamo mostrato il grafico anche per valori negativi di $\abs{\phi}$ per dare meglio l’idea, ma ovviamente $\abs{\phi} \geq 0$. Notiamo che dobbiamo avere $\lambda > 0$, altrimenti il potenziale non ha minimo inferiore e quindi la teoria sarebbe instabile.
Se la simmetria $U(1)$ fosse una simmetria globale, diremmo che nel secondo caso ($\mu < 0$) c’è rottura spontanea di simmetria: abbiamo un minimo per ogni $\phi = \sqrt{-\frac{\mu}{2\lambda}} e^{i \xi}$ per una qualsiasi fase $\xi$, ovvero infiniti minimi. A energie sufficientemente basse, il sistema finirà in uno di questi minimi, diciamo quello per $\xi = \xi_0$. Una trasformazione $U(1)$ cambierebbe $\xi_0$, per cui non possiamo più effettuarla: la simmetria è rotta.
Questa analisi non vale nel caso di una teoria di calibro. Poiché i vari stati con diversi valori di $\xi$ sono collegati tra loro da una simmetria di calibro, sono effettivamente lo stesso stato: il vuoto è unico e non c’è rottura spontanea di simmetria. Notiamo inoltre che sebbene nel vuoto $\langle \abs{\phi}\rangle \neq 0$, $\abs{\phi}$ è invariante rispetto alle trasformazioni di calibro e può pertanto acquisire un valore atteso non-nullo senza violare il teorema di Elitzur. Anche quando $\langle \abs{\phi} \rangle \neq 0$ abbiamo comunque $\langle \phi \rangle=0$ e ciò non ci sorprende perché $\phi$ non è invariante di calibro.
Tutto il meccanismo di Higgs sta nell’osservazione che il campo di Higgs acquisice un valore atteso non-nullo (la famosa “VEV”, dall’inglese “vacuum expectation value”). Non c’è rottura spontanea di nessuna simmetria.
Viene talvolta detto che il gruppo che si rompe sarebbe la parte globale della simmetria locale $U(1)$, cioè quel sottoinsieme di tutte le simmetrie di calibro che sono uguali in ogni punto dello spaziotempo. Tuttavia anche questo non è vero: la simmetria “globale” $U(1)$ è anch’essa una simmetria di calibro e non è rotta. Infatti il “parametro d’ordine” che acquisice un valore atteso non-nullo, cioè $\abs{\phi}$, è invariante rispetto a tutte le trasformazioni $U(1)$, globali o locali. D’altronde, è assurdo che si possa rompere la parte globale ma non quella locale: possiamo infatti effettuare due trasformazioni locali appositamente scelte, la cui somma è una trasformazione globale. Poiché le due sono locali non rompono nulla, e quindi la loro somma non può rompere nulla.
Cosa succede nella Lagrangiana?
Ora vediamo cosa succede nella Lagrangiana. Espandiamo la teoria attorno al minimo:
$$\phi=(\rho_0+\rho(x))e^{i \xi(x)}$$
dove $\rho_0=\sqrt{-\frac{\mu}{2\lambda}}$. Nel fare ciò l’unica cosa che supponiamo è che $\rho_0 \neq 0$, cioè che il bosone di Higgs abbia un valore atteso non-nullo. Nel primo caso ($\mu > 0$) il minimo sarebbe a $\rho_0$ e non guadagniamo nulla da questa espansione. Sostituendo otteniamo:
$$\mathcal{L} = -\frac{1}{4} F_{\mu\nu} F^{\mu\nu} + \partial^\mu \rho \partial_\mu \rho + (\rho_0+\rho)^2 \partial^\mu \xi \partial_\mu \xi -2 e A^\mu \partial_\mu \xi (\rho_0+\rho)^2 + e^2 A_\mu A^\mu (\rho_0+\rho)^2 -\mu \pqty{\rho_0+\rho}^2 -\lambda \pqty{\rho_0+\rho}^4$$
In altre parole abbiamo ottenuto un campo scalare reale massivo ($\rho$), un campo scalare reale a massa nulla ($\xi$), più una serie di complicate interazioni. Abbiamo anche ottenuto un termine $e^2 A_\mu A^\mu (\rho_0+\rho)^2$, espandendo il quale otteniamo una massa per $A_\mu$. Inoltre la Lagrangiana sopra è ancora invariante di calibro:
$$A_\mu \to A_\mu + \partial_\mu \alpha\,\,\,\,\,\,\,\,\, \xi \to \xi + e \alpha$$
Notiamo che $\xi$ non è un bosone di Goldstone. Lo sarebbe stato se avessimo rotto una simmetria globale, ma ciò non è il caso. In particolare, non è un campo invariante di calibro.
Volendo possiamo anche scegliere un calibro specifico, e il più conveniente è quello per cui $\xi \equiv 0$. In questo caso la Lagrangiana diventa:
$$\mathcal{L} = -\frac{1}{4} F_{\mu\nu} F^{\mu\nu} + \partial^\mu \rho \partial_\mu \rho + e^2 A_\mu A^\mu (\rho_0+\rho)^2 -\mu \pqty{\rho_0+\rho}^2 – \lambda \pqty{\rho_0+\rho}^4$$
Questa Langrangiana non è più invariante di calibro perché abbiamo fissato il calibro a mano. In questo calibro, la descrizione fisica è che il campo di calibro $A_\mu$ ha “mangiato” il “bosone di Goldstone” $\xi$. Enfatizziamo di nuovo che non c’è stata nessuna rottura spontanea di simmetria, e che $\xi$ non è un bosone di Goldstone: in questo calibro non esiste neanche.
Una descrizione invariante di calibro
Possiamo trovare una descrizione invariante di calibro della situazione? La risposta per fortuna è sì. Partendo dalla teoria originale con $\phi$, $A_\mu$, definiamo tre nuovi campi $\rho, \xi, B_\mu$:
$$\phi = \rho e^{i\xi}\,\,\,\,\,\,\,\,\,\,\,\,B_\mu = A_\mu -\frac{1}{e} \partial_\mu \xi$$
La bellezza di questi campi (facilmente verificabile) è che tutte le trasformazioni di calibro sono assorbite in $\xi$: tanto $B_\mu$ quanto $\rho$ sono invarianti di calibro, mentre $\xi$ trasforma come al solito. Sostituendo nella Lagrangiana originale otteniamo:
$$\mathcal{L} = -\frac{1}{4} \widetilde{F}_{\mu\nu} \widetilde{F}^{\mu\nu} + \partial^\mu \rho \partial_\mu \rho + e^2 \rho^2 B_\mu B^\mu -\mu \rho^2 – \lambda \rho^4=\\
=-\frac{1}{4} \widetilde{F}_{\mu\nu} \widetilde{F}^{\mu\nu} + \widetilde{D}^\mu \rho \widetilde{D}_{\mu}^* \rho -\mu \rho^2 – \lambda \rho^4$$
dove la tilda sta a indicare la “derivata covariante” e il “tensore elettromagnetico” per $B_\mu$.
Sorpresa: il campo $\xi$ è sparito. In altre parole, questa Lagrangiana è del tutto invariante di calibro rispetto alla simmetria $U(1)$ iniziale. La descrizione in questo caso è di nuovo: il bosone vettore ha mangiato “il bosone di Goldstone”. Ma ovviamente il bosone di Goldstone non esiste (come è evidente in questa descrizione) perché non c’è rottura spontanea di simmetria. Se $\rho$ fosse un campo complesso, di nuovo avremmo un’altra simmetria $U(1)$, ma $\rho$ è reale e positivo, perciò non c’è nessuna simmetria di calibro.
Ora la descrizione è evidente: abbiamo un unico minimo $B_\mu=0$ e $\rho = \rho_0 \neq 0$ e quindi un unico vuoto. Pertanto non ci può essere nessuna rottura spontanea di simmetria, ma poiché $\rho_0 \neq 0$, il bosone vettore acquisice una massa.
Conclusione
In conclusione, il meccanismo di Higgs consiste nell’affermazione che un valore atteso di vuoto non-nullo del campo di Higgs dà massa ai bosoni vettori. Al contempo, come abbiamo visto, non c’è rottura spontanea della simmetria di calibro, il che sarebbe assurdo, perché la simmetria di calibro è solo una ridondanza nella nostra descrizione della natura fisica.
Non sappiamo perché l’Higgs abbia un valore atteso di vuoto non nullo. Però questo fatto è perfettamente compatibile con la simmetria di calibro.
In conclusione, nella rottura spontanea di una simmetria globale $G \to H$, dove $H$ è la simmetria residua, abbiamo:
- $\mathrm{dim}(G)-\mathrm{dim}(H)$ bosoni di Goldstone a massa nulla;
- il vuoto della teoria non è più simmetrico rispetto a $G$, ma è ancora simmetrico rispetto ad $H$.
Al contrario, con “rottura spontanea” di una simmetria di calibro $G \to H$, dove $H$ è la simmetria residua, intendiamo che solo alcuni componenti del campo di Higgs acquisiscono un valore atteso non-nullo. In questo caso abbiamo:
- $\mathrm{dim}(G)-\mathrm{dim}(H)$ bosoni vettori, prima senza massa, ora massivi;
- altri $\mathrm{dim}(H)$ bosoni vettori che rimangono a massa nulla;
- il vuoto della teoria rimane simmetrico rispetto all’intero gruppo $G$.
In quest’ultimo caso, propriamente parlando non c’è “rottura spontanea”, perché il vuoto rimane invariante.
