In un precedente articolo, abbiamo visto il più semplice modello epidemiologico, cioè il modello SIS. Una delle ipotesi del modello è che il tasso di guarigione delle persone infette, cioè $\alpha$, è una costante indipendente sia da $I$, il numero di persone infette, sia da $S$, il numero di persone suscettibili alla malattia.
Tuttavia, se il numero di infetti è molto alto, gli ospedali saranno sovraffollati e quindi la qualità delle cure diminuirà, e con essa il tasso di guarigione. In questo articolo cercheremo di incorporare questo effetto nel modello SIS. In particolare modificheremo il tasso di guarigione in modo che dipenda dal numero degli infetti:
$$\alpha(I) = \frac{\alpha}{1+I}$$
In questa maniera $\alpha = \alpha(0)$ è il tasso di guarigione massimo, raggiunto nella migliore delle condizioni, cioè quando non ci sono infetti. Quando $I$ aumenta, il tasso di guarigione diminuisce. Chiaramente anche questa è un’approssimazione rozza, ma anche con una funzione così semplice l’analisi diventa abbastanza complicata. Le equazioni che descrivono il modello diventano:
$$ S'(t) = -\beta I S +\frac{\alpha I}{1+I}\\
I'(t) = \beta I S -\frac{\alpha I}{1+I}$$
Abbiamo ancora $S'(t)+I'(t) =0$, per cui possiamo sostituire $S$ e ottenere una singola equazione per $I$:
$$I'(t) = \beta I (N-I) -\frac{\alpha I}{1+I}$$
Potremmo risolvere esplicitamente questa equazione, ma la soluzione è talmente complicata da essere inutile. Ci concentriamo invece sullo studio delle situazioni di equilibrio. Perciò basta impostare $I’=0$ e vedere che tipo di soluzioni abbiamo. Poniamo $r = \beta N -\alpha$ e $K = r/\beta = N-\alpha/\beta$ come nel precedente articolo. Nel caso precedente, il modello SIS senza saturazione delle cure, avevamo due casi:
- Se $r>0$ allora la malattia diventa endemica e il numero di infetti si stabilizza su $I=K$.
- Se $r < 0$ allora la mattia svanisce dalla popolazione e il numero di infetti si stabilizza su un valore nullo.
Ora vediamo che succede con l’aggiunta della saturazione delle cure. Per trovare gli equilibri poniamo $I’=0$. Una soluzione è $I=0$, ma abbiamo anche altre due soluzioni:
$$I_\pm = \frac{(N-1) \pm \sqrt{(N-1)^2 + 4 K}}{2}$$
Ora cercheremo di capire se queste tre soluzioni sono stabili o meno. Poniamo $I'(t) = f(I)$. Come abbiamo visto in un precedente articolo, si tratta di determinare il segno della derivata $f'(I^*)$ dove $I^*$ è il punto di equilibrio.
Il calcolo analitico di queste cose è abbastanza complicato. Possiamo però indovinare il grafico di $f(I)$ e di lì il segno della derivata. I calcoli sono abbastanza noiosi e non li mostreremo qui. Bisogna notare che per $I \to \pm \infty$ abbiamo $f(I) \to -\infty$, e inoltre effettuare lo studio del segno di $f(I)$, che è noioso ma elementare e non troppo complicato. Segue che il grafico di $f(I)$ ha la forma qualitativa seguente:
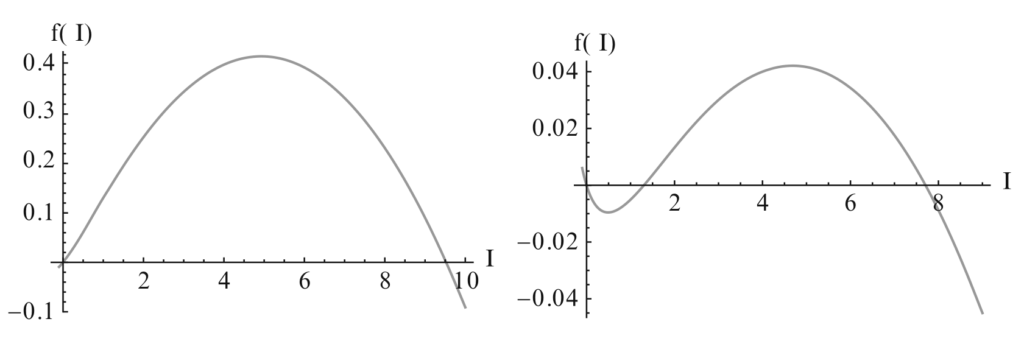
A sinistra $r > 0$, a destra $r<0$. Presa da Martcheva, An Introduction to Mathematical Epidemiology.
I punti di equilibrio hanno $f(I)=0$. Come abbiamo visto nell’ultimo articolo citato, se $f(I)$ è crescente in un punto di equilibrio $I^*$ allora $f'(I^*) > 0$ e quindi il punto di equilibrio è instabile; se invece decresce la derivata è negativa e il punto è stabile. Troviamo pertanto quanto segue:
- Se $r > 0$, allora $K > 0$. Quindi il numero dentro la radice è sempre positivo, e quindi entrambe le soluzioni $I_\pm$ sono reali. Tuttavia in questo caso $I_- < 0$, e quindi non è permessa. Abbiamo quindi due equilibri, $I = I_+$ (stabile) oppure $I=0$ (instabile). L’epidemia si stabilizza quindi su $I=I_+$ e diventa endemica. Notiamo inoltre che $I_+ > K$, per cui il numero stabile di infetti è maggiore che nel caso senza saturazione delle cure, come ci aspettavamo.
- Se $r < 0$ allora abbiamo due casi. Se $\alpha/\beta > (N+1)^2/4$, allora il numero dentro la radice è negativo. Quindi l’unico equilibrio è $I=0$, che è stabile. Poiché $N$ è la popolazione, possiamo immaginarcelo come un numero grande; quindi la condizione $\alpha/\beta > (N+1)^2/4$ vuol dire $\alpha \gg \beta$, cioè il tasso di guarigione è molto più elevato del tasso di contagio. In questo caso ha senso ciò che accade: l’epidemia sparisce.
- Se invece $r < 0$ ma $\alpha/\beta < (N+1)^2/4$, allora le due soluzioni $I_\pm$ sono permesse ed entrambe positive. Tuttavia $I_-$ è instabile e abbiamo quindi due equilibri stabili, $0$ e $I_+$. In quale dei due andiamo a finire? Dipenderà dalle condizioni iniziali: se la condizione iniziale è $I=I_0$ allora per $0 < I_0 < I_-$ saremo attratti dall’equilibrio $I=0$ e la malattia sparirà. Se invece inizialmente $I_- < I_0 < I_+$, allora saremo attratti da $I_+$ e la malattia diventerà endemica. Questo (pur in un modello semplificato) mostra l’importanza del controllo delle malattie nelle fasi iniziali.
Ricordiamo che il numero riproduttivo di base è $R_0 = N\frac{\beta}{\alpha}$ e dipende solo da $r$ e $N$. In particolare $r > 0$ corrisponde a $R_0 > 1$, mentre $r < 0$ corrisponde a $R_0 < 1$.
Riassumendo, nel caso in cui il numero riproduttivo di base $R_0 > 1$ (quindi $r > 0$) l’epidemia diventerà endemica come nel caso senza saturazione, ma un maggior numero di persone contrarrà la malattia nella fase di equilibrio. Inoltre se le cure saturano allora anche per $R_0 < 1$ è possibile che la malattia diventi endemica, e ciò dipende dal numero iniziale di contagiati.. Al contrario, nel caso senza saturazione, se $R_0 < 1$ l’epidemia sparisce automaticamente.
