Il modello SIS è uno dei modelli epidemiologici più semplici, e si applica a quelle malattie per cui non sviluppiamo nessuna immunità dopo averle contratte, e quindi è possibile prenderle più volte.
La popolazione totale, $N$, è fissa. Il numero di persone infette dalla malattia è $I$, che sta appunto per “infetto”. Poiché non c’è immunità, tutti quelli che non sono infetti sono almeno suscettibili, cioè possono contrarla, e questa popolazione la chiamiamo $S$.
Il numero di infetti e suscettibili varia col tempo, $S = S(t)$ e $I = I(t)$, ma per ipotesi la popolazione totale $N$ è fissa. Stiamo cioè ignorando nascite e morti, che può essere una buona approssimazione dato che queste sono piccole percentuali sul totale della popolazione. Abbiamo quindi $S(t)+I(t) = N$.
Ora formuleremo delle equazioni per $S$ e $I$. Vogliamo capire come variano $S$ e $I$. Ci sono due maniere in cui una persona può passare da $I$ ad $S$ e viceversa: un’individuo in $S$ può contrarre la malattia, e quindi diventare infetto e passare in $I$; oppure un’individuo infetto, cioè in $I$, può guarire e quindi passare in $S$. Chi guarisce infatti diventa immediatamente suscettibile, non essendoci immunità. La situazione è illustrata nel diagramma seguente:
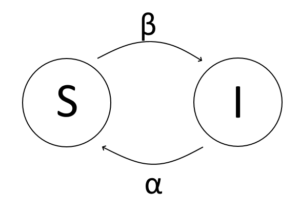
Consideriamo prima di tutto la guarigione. Ad ogni istante di tempo una certa frazione $\alpha$ delle persone infette guarirà. Per cui ad ogni istante di tempo gli infetti diminuiranno di $\alpha I$, mentre i suscettibili aumenteranno di $\alpha I$. Possiamo supporre che il tasso di guarigione $\alpha$ sia costante, poiché la guarigione è un processo intrinseco agli infetti e non dipende né da $S$ né da $I$. Questa è un’approssimazione: ad esempio il tasso di guarigione dipenderà dal tipo di cure che si ricevono; ma se $I$ è molto grande, allora gli ospedali saranno saturi e quindi le cure ricevute peggioreranno. Tratteremo questa situazione più avanti, ma per adesso $\alpha$ è una costante.
Consideriamo ora il contagio. Ad ogni istante di tempo il numero di persone contagiate sarà proporzionale ad $S$, il numero di suscettibili. Tuttavia, al contrario di sopra, il tasso di contagio non è indipendente da $I$. Infatti se ci sono più infetti nella popolazione, allora il numero di contagiati ad ogni istante di tempo sarà maggiore. Pertanto il numero di contagiati in ogni istante di tempo sarà $\beta I S$ dove $\beta$ è una costante detta tasso di trasmissione.
Mettendo insieme i due meccanismi, abbiamo le due seguenti equazioni:
$$ S'(t) = -\beta I S +\alpha I\\
I'(t) = \beta I S -\alpha I$$Ci rassicura notare che $S'(t) + I'(t) = 0$, così la popolazione totale $S+I = N$ è costante. Utilizzando quest’ultima equazione possiamo rimuovere una delle variabili, ottenendo:
$$I'(t) = \beta I (N-I) -\alpha I$$
Raccogliendo alcuni termini otteniamo la seguente forma,
$$I'(t) = r I \pqty{1-\frac{I}{K}}$$
dove $r = \beta N -\alpha$ e $K = r/\beta = N-\alpha/\beta$. Questa equazione è nota come l’equazione logistica, ed è molto comune nella descrizione delle dinamiche di popolazione. Il parametro $r$ è particolarmente importante, ed è detto tasso di crescita. Infatti abbiamo due casi:
- Se $r < 0$, allora $I(t) \to 0$ per $t \to \infty$, cioè la malattia sparirà dalla popolazione.
- Se invece $r > 0$ allora $I(t) \to K$ per $t \to \infty$, cioè la malattia rimarrà indefinitamente nella popolazione.
Per ottenere questi risultati risolviamo direttamente l’equazione differenziale, tramite separazione delle variabili. Abbiamo:
$$\frac{dI}{I \pqty{1-\frac{I}{K}}} = r dt$$
Possiamo quindi utilizzare la scomposizione in frazioni parziali
$$\frac{1}{I \pqty{1-\frac{I}{K}}} = \frac{1}{I} + \frac{1}{K-I}$$
e quindi integrando otteniamo
$$\log I -\log\abs{K-I} = rt + C$$
Quindi risolvendo per $I$ otteniamo
$$ I(t) = \frac{KB e^{rt}}{1+ B e^{rt}}$$
dove $B$ è una costante qualsiasi. Dalla soluzione esplicita segue il risultato che abbiamo preannunciato: se $r < 0$ la malattia sparirà dalla popolazione, mentre se invece $r > 0$ si raggiungerà un equilibrio dinamico in cui $K$ persone avranno sempre la malattia, che diventa endemica. Il grafico sotto mostra alcune soluzioni:
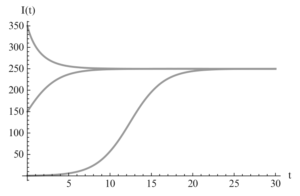
Presa da Martcheva, An Introduction to Mathematical Epidemiology.
Notiamo che la condizione $r > 0$ può anche essere riscritta come
$$R_0 = N\frac{\beta}{\alpha} > 1$$
dove $R_0$ è il numero riproduttivo di base, ed è il numero di infezioni secondarie causate da un singolo individuo infetto in una popolazione interamente suscettibile. Come abbiamo visto prima il numero di infezioni per unità di tempo è $\beta I S$. Se c’è un singolo individuo infetto $I=1$, mentre $S=N$ poiché l’intera popolazione è suscettibile. Quindi il numero di infezioni per unità di tempo è $\beta N$; poiché il tasso di guarigione è $\alpha$, l’individuo rimarrà infetto per un tempo $1/\alpha$ e quindi in totale infetterà $\beta N /\alpha = R_0$ individui suscettibili.
