Nello scorso articolo abbiamo effettuato la rinormalizzazione del modello di Sine-Gordon, e abbiamo trovato le funzioni beta
$$\dv{\lambda}{s} = \pqty{2-\frac{g^2}{4\pi}}\lambda\\ \dv{g}{s} = -f(g) g^3 \lambda^2$$
dove $f(g)$ è una funzione complicata ma positiva. Ora vediamo le conseguenze di quanto abbiamo trovato.
Innanzitutto ricordando che $g \sim \sqrt{J}$, troviamo un’altra interpretazione della transizione: cioè il gas di vortici e antivortici riduce la “rigidità” $J$ delle onde di spin, schermando gli spin.
Per proseguire con l’analisi, conviene scrivere
$$g = \frac{2\pi}{\sqrt{K}}$$
Otteniamo quindi
$$\dv{\lambda}{s} = \pqty{2-\frac{\pi}{K}}\lambda\\ \dv{K}{s} = 8\pi^2 f \lambda^2$$
Disegnando i flussi otteniamo qualcosa del genere:
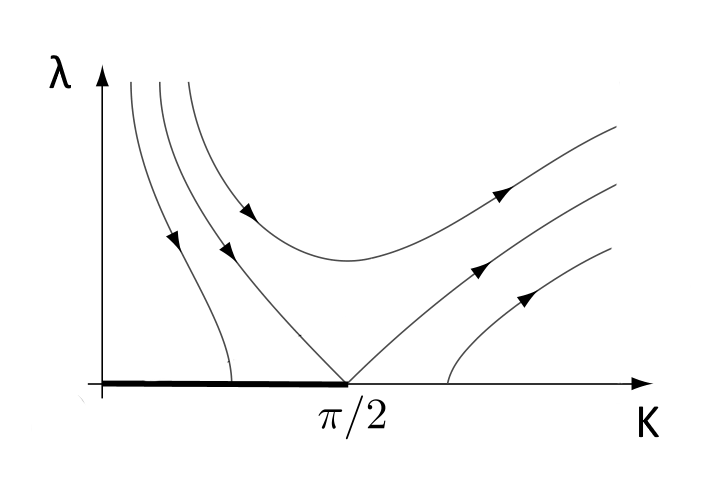
Adattata da Altland & Simons.
La regione in $\lambda = 0$ evidenziata (cioè da $K=0$ a $K=\pi/2$) corrisponde alla regione dove il decadimento della funzione della correlazione è una potenza, mentre la regione $K > \pi/2$ corrisponde al decadimento esponenziale. La transizione di fase avviene in $K=\pi/2$.
Possiamo ora concentrarci sulla transizione di fase. Poniamo
$$K = \frac{\pi}{2}+x\\
\lambda = \frac{1}{\sqrt{8\pi f}}y$$
Allora otteniamo
$$\dv{x}{s} = y^2 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \dv{y}{s} \approx \frac{4}{\pi}xy$$
Otteniamo quindi che
$$\dv{(x^2)}{s} = 2xy^2 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \dv{(y^2)}{s} \approx \frac{2}{\pi}xy^2$$
ovvero
$$\dv{}{s} \pqty{x^2-\pi y^2}=0$$
Quindi vicino al punto critico le linee del flusso di rinormalizzazione sono iperboli parametrizzate da $\rho = x^2-\pi y^2$:
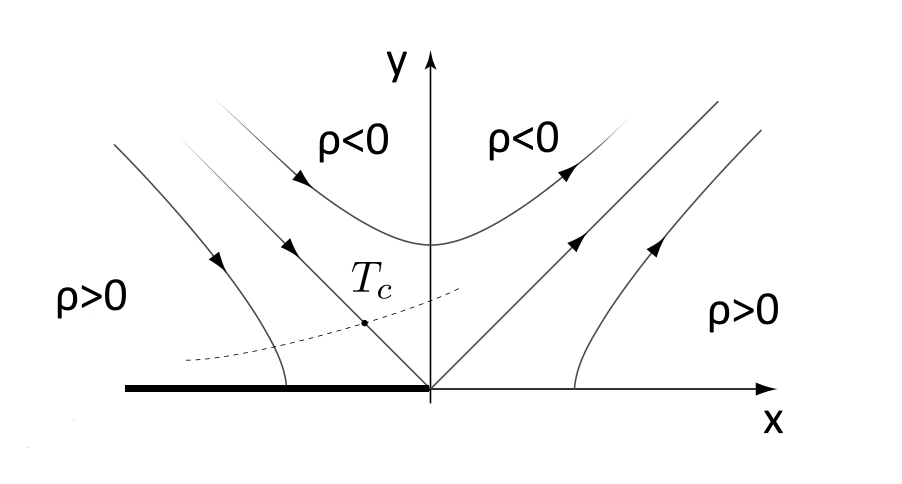
Per $\rho > 0$ abbiamo due regioni: la regione a bassa temperatura, dove $\lambda$ (cioè $y$) viene mandata rapidamente a zero e $K$ (cioè $x$) viene mandato ad un valore finito, e la regione ad alta temperatura dove sia $\lambda$ che $K$ vanno ad infinito.
Le due rette $\rho=0$ fluiscono una direttamente al punto critico, e l’altra esce dal punto critico, con $x = \pm \sqrt{\pi} y$. Ciò vuol dire, incidentalmente, che una fugacità piccola ma non nulla riduce la temperatura critica: in altre parole, se il modello è descritto da parametri dovunque sulla retta $x = -\sqrt{\pi} y$, allora sarà equivalentemente descritto dalla teoria al punto critico.
Per $\rho < 0$ non raggiungiamo mai il punto critico e il flusso descresce ad un valore minimo di $\lambda$ e poi va all’infinito.
Possiamo pensare al processo nella maniera seguente. Partiamo da un certo punto $(x_0, y_0)$ del diagramma, determinato dalla temperatura a cui ci troviamo $(x_0(T), y_0(T))$. Infatti le costanti $\lambda$ e $K$ oltre a dipendere dai parametri del modello (che si suppongono fissati) dipendono anche dalla temperatura. Dal punto $(x_0(T), y_0(T))$ seguiamo il flusso di rinormalizzazione e andiamo a finire nella regione a bassa temperatura, nella regione ad alta temperatura, o nel punto critico. Dove andremo a finire è determinato dal segno di $\rho(T)$ come funzione di $T$. Espandendo in serie vicino al punto critico, troviamo che $\rho(T) \approx \rho_0(T_c-T)$ dove $\rho_0$ è una costante positiva, in modo da riprodurre il comportamento che cerchiamo.
Possiamo quindi calcolare la lunghezza di correlazione. Consideriamo un flusso con $\rho < 0$, così che non andiamo a colpire il punto critico. Abbiamo quindi
$$\dv{x}{s} = y^2 = \frac{1}{\pi}(x^2+|\rho|)$$
Risolvendo l’equazione differenziale otteniamo
$$s = \frac{\pi}{\sqrt{|\rho|}}\bqty{\arctan{\pqty{\frac{x}{\sqrt{\abs{\rho}}}}}-\arctan{\pqty{\frac{x_0}{\sqrt{\abs{\rho}}}}}}$$
Chiaramente questa è solo un’approssimazione; ad esempio per $x \to \infty$ abbiamo che $s$ tende ad un valore finito. Tuttavia possiamo usarla per stimare il comportamento della lunghezza di correlazione. In particolare, una volta che siamo arrivati ad $x \approx 1$ siamo ben oltre la validità dell’approssimazione e fermiamo il flusso.
Poiché la lunghezza di correlazione è una lunghezza, allora scala come
$$\xi \sim e^s \sim \exp{\pqty{\frac{1}{\sqrt{\abs{\rho}}}}}\sim \exp{\pqty{\frac{1}{\sqrt{T-T_c}}}}$$
Dato che siamo in $2D$ e l’energia libera è una quantità estensiva, allora scala come $L^2/\xi^2$. Infatti abbiamo che l’energia libera per volume è $f \sim \frac{1}{V}\log{Z}$, ma la funzione di partizione è invariante, quindi $f \sim \frac{1}{V} \sim \frac{1}{\xi^d}$ in $d$ dimensioni. Abbiamo quindi
$$F \sim \exp{\pqty{-\frac{1}{\sqrt{T-T_c}}}}$$
Questa è una funzione ben particolare: abbiamo un punto di non-analicitià quando avviene la transizione di fase, però tutte le derivate esistono ad ogni ordine, per cui in un certo senso la transizione è “di ordine infinito”.
