L’effetto Einstein-de Haas è un effetto piuttosto strano che avviene quando si mette un ferromagnete (ad esempio una barretta di ferro) in un campo magnetico. La barretta di ferro immersa nel campo magnetico infatti comincerà a ruotare. L’effetto funziona anche al contrario: una barretta rotante genererà un campo magnetico, e in questo caso si parla di effetto Barnett.
L’esperimento è come nell’immagine seguente:
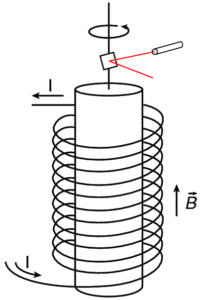
Ovvero abbiamo la nostra barretta di metallo all’interno di un solenoide. Se non passa corrente non succede niente, mentre se passa corrente il solenoide genera un campo magnetico. A questo punto la barretta comincerà a ruotare e la rotazione può essere misurata sparando un laser su uno specchio che ruota insieme alla barretta. Possiamo vedere l’effetto in azione in questo video:
La barretta si muove avanti e dietro perché la corrente nell’esperimento è alternata e quindi cambia direzione, facendo cambiare direzione anche al campo magnetico.
Qual è la spiegazione del fenomeno? L’effetto ha che fare con lo spin degli elettroni all’interno del ferromagnete. Una qualsiasi particella carica in moto attorno ad un certo asse genererà un momento di dipolo magnetico proporzionale al momento angolare del moto, $\vec{\mu} \propto \vec{J}$.
Per un elettrone la relazione più precisa è data da $\vec{\mu} =g \frac{e}{2m} \vec{j}$ dove $g$ è il cosiddetto fattore giromagnetico o fattore-g. È una vecchia storia della meccanica quantistica che se $\vec{j}$ è il momento angolare orbitale allora $g \approx 1$ come ci aspetteremmo classicamente; se invece $\vec{j}$ è lo spin dell’elettrone allora $g\approx 2$, che è “anomalo”. L’effetto Einstein-de Haas mostra che $g \approx 2$ e quindi la rotazione è dovuta prevalentemente allo spin degli elettroni.
Per spiegare l’effetto pensiamo in maniera classica. Senza campo magnetico lo spin degli elettroni è disposto a caso, per cui sommando i contributi di tutti gli elettroni nel materiale otteniamo che la magnetizzazione totale è nulla: $\vec{M}=0$. Con l’introduzione del campo magnetico gli elettroni si allineeranno tutti nella stessa direzione e quindi i vari contributi si sommano e otteniamo una magnetizzazione non-nulla $\vec{M} = g \frac{e}{2m} \vec{J}$ dove stavolta $\vec{J}$ è il momento angolare macroscopico dell’oggetto. (anche se non dovremmo, immaginiamo gli elettroni come delle sferette che girano, il cui momento angolare è allineato a quello dell’oggetto macroscopico). Per un ferromagnete $\vec{M} \propto \vec{B}$.
Il campo magnetico non esercita nessun momento torcente perché $\vec{\mu}$ e $\vec{B}$ sono allineati, quindi il momento angolare è conservato. Dato che inizialmente l’oggetto non aveva momento angolare e adesso ha acquisito un momento angolare non-nullo a causa dell’allineamento degli elettroni, dovrà cominciare a ruotare con momento angolare opposto $-\vec{J}$.
Misurando l’angolo massimo di rotazione si può quindi determinare $g$, e si trova $g \approx 2$. Se ne deduce che l’effetto è dovuto prevalentemente allo spin degli elettroni.
