Negli articoli precedenti abbiamo impostato la discussione della transizione BKT e posto alcune questioni fondamentali. In questo articolo vedremo come la transizione è originata dalla proliferazione di “difetti topologici” detti “vortici”.
Vortici e difetti topologici
Ma quindi in pratica cosa succede? La transizione BKT è essenzialmente dovuta ai cosiddetti “vortici”. Quando siamo nella fase ad alta temperatura, i vortici sono liberi di muoversi in giro e disordinano gli spin causando la fase disordinata. Sotto una certa temperatura critica, i vortici “condensano”: ovvero i vortici saranno vincolati in coppie con “carica opposta”, annullando l’effetto totale sul sistema e permettendo una fase in un qualche senso ordinata.
Vediamo la cosa più da vicino. Finora abbiamo ignorato il fatto che $\theta$ è una variabile angolare in $[0,2\pi]$, ma ora questo fatto avrà una valenza cruciale. Partendo dall’Hamiltoniana $(1)$, cioè
$$\mathcal{H} =\frac{J}{2} \int d^2 x\, \pqty{\nabla \theta}^2$$
otteniamo subito l’equazione del moto per $\theta$, che è l’equazione di Laplace,
$$\nabla^2 \theta = 0$$
Il fatto che $\theta$ è una variabile angolare implica che
$$\oint_C \nabla \theta \cdot d\vec{s} = \theta(2\pi) -\theta(0)=2\pi n$$
cioè le soluzioni devono avere una “circolazione” data da un multiplo di $2\pi$. Questo perché $\theta$ è una variabile periodica, per cui dopo un giro completo deve tornare a se stessa modulo $2\pi$. Tra queste configurazioni, ce ne saranno chiaramente molte la cui circolazione è nulla ($n=0$). Tuttavia ciò non è necessario, e ci saranno anche delle configurazioni con $n \neq 0$. Il numero $n$ è detto in matematica anche numero di avvolgimento, e le configurazioni con $n \neq 0$, dette vortici, sono pertanto “topologicamente non banali”.
In termini più concreti, consideriamo la situazione in cui abbiamo un solo vortice nell’origine. Poi generalizzeremo la discussione al caso multi vortice. Nelle coordinate polari $(r,\varphi)$ del piano, una soluzione dell’equazione di Laplace con circolazione $n$ è data da
$$\theta = \theta_0 + n\varphi \tag{3}$$
Questa soluzione è singolare nell’origine, ma ciò non si può evitare, come vedremo poi. In particolare l’origine può essere pensata come il nucleo centrale del vortice, dove non sappiamo cosa succede e su ciò rimarremo ignoranti. Possiamo visualizzare queste soluzioni in alcuni casi particolari:
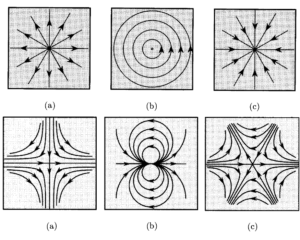
Immagine presa da Chaikin & Lubensky.
Le figure (a), (b) e (c) sulla prima riga rappresentano tre configurazioni di vortici come nell’equazione $(3)$ con $n=1$ e $\theta_0=0, \pi/2, \pi$ rispettivamente. Le figure (a), (b) e (c) della seconda riga sono invece vortici con $n=-1, 2, -2$ rispettivamente.
La figura (b) della prima riga è quello che ci immaginiamo tipicamente quando parliamo di vortici, che però possono assumere anche forme diverse, come nelle altre figure.
Le soluzioni della forma $(3)$ sono di carattere illustrativo, ma ovviamente non tutte le soluzioni di vortici sono di quella forma, e ne esistono di più generali.
Derivazione della transizione nel caso a singolo vortice
Rimettendo la soluzione $(3)$ nell’Hamiltoniana possiamo calcolare l’energia di un vortice $E_v$:
$$E_v = E_{\mathrm{nucleo}}+ \frac{J}{2} \int_{a < r < L} d^2 x\, \pqty{\nabla \theta}^2 = E_{\mathrm{nucleo}} + \pi n^2 J \log{\pqty{\frac{L}{a}}}$$
dove abbiamo limitato l’integrazione all’intervallo $a < r < L$ per evitare divergenze. In particolare $L$ può essere pensato come la dimensione del sistema in esame, e $a$ è la dimensione del nucleo del vortice: per cui abbiamo rimpiazzato l’integrazione con $r < a$ con l’energia del nucleo $E_{\mathrm{nucleo}}$. Possiamo pensare a $E_{\mathrm{nucleo}}$ come ad una quantità molto grande, per cui non avrà dipendenze rilevanti rispetto ai vari parametri.
Notiamo innanzitutto che l’energia del vortice va come $n^2$. Ciò vuol dire che i vortici con $|n| > 1$ sono soppressi e quindi al massimo si formeranno vortici con $n=\pm 1$, che chiameremo “vortici” e “antivortici”.
Ora supponiamo di avere di un sistema senza vortici e di volerci mettere un vortice. Se l’energia libera totale del sistema aumenta, allora il cambiamento sarà soppresso, se invece l’energia libera diminuisce, la formazione di un vortice sarà favorita. Abbiamo
$$\Delta F = \Delta E -T \Delta S$$
Abbiamo $\Delta E = \pi J \log{\pqty{\frac{L}{a}}}$. Per calcolare l’entropia, sappiamo che il vortice ha grandezza tipica $a$ e che può finire in un campione bidimensionale di lunghezza $L$: per cui abbiamo circa $L^2/a^2$ possibili modi di mettere il vortice nel sistema, e quindi un’entropia di $k_B \log{(L^2/a^2)}$.
Non abbiamo introdotto l’energia del nucleo in $\Delta E$ perché non cambia l’analisi qualitativa del sistema. Infatti sebbene $E_{\mathrm{nucleo}}$ è molto grande, anche $ \log{\pqty{\frac{L}{a}}}$ è molto grande e quindi l’effetto di aggiungere l’energia del nucleo è fornire una correzione alla temperatura critica della transizione. Includeremo questo effetto nell’analisi finale che effettueremo nei prossimi articoli.
Mettendo insieme otteniamo
$$\Delta F = (\pi J -2k_B T) \log{\pqty{\frac{L}{a}}}$$
per cui vediamo che c’è una transizione di fase alla temperatura critica
$$k_B T_c = \pi\frac{J}{2}$$
Sotto questa temperatura la formazione di vortici è soppressa, e quindi il sistema è superfluido. Sopra questa temperatura i vortici proliferano e distruggono il quasi-ordine.
Nel prossimo articolo vedremo come generalizzare la discussione al caso con $n$ vortici, e troveremo che sarà equivalente ad un noto modello di fisica statistica dei campi.
