Nel precedente articolo abbiamo impostato il problema del calcolo della radiazione di Hawking secondo il metodo originale dell’autore. Procediamo direttamente da dove avevamo lasciato.
Per ottenere una relazione tra le $\alpha$ e le $\beta$ procediamo nel modo seguente. Consideriamo un’onda $g_\omega$ su $\mathscr{I}^+$ e cerchiamo di capire da quale onda su $\mathscr{I}^-$ è originata. Applichiamo la cosiddetta approssimazione dell’ottica geometrica (che vedremo nel dettaglio fra poco) secondo cui un’onda a fase costante viaggia lungo geodetiche nulle. Poiché nel nostro caso l’onda è radiale, viaggerà lungo geodetiche nulle radiali. Un esempio di traiettoria è mostrato nella figura sotto, ricordando che le geodetiche radiali nulle hanno un angolo di $\pm 45^\circ$ nel diagramma di Penrose:
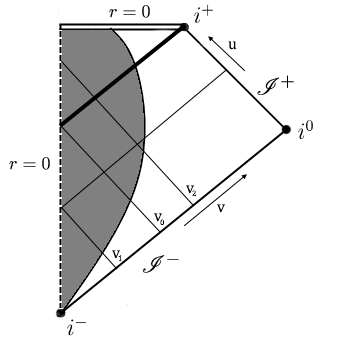
Nel disegno sono rappresentate tre onde che partono da $\mathscr{I}^-$. La prima parte da $v = v_1$, passa attraverso il corpo durante il collasso, prosegue come onda uscente e termina su $\mathscr{I}^+$. L’onda che parte da $v=v_2$ invece arriva al corpo in collasso troppo tardi, ed entra nell’orizzonte degli eventi. Il punto $v=v_0$ è il limite di separazione dei due casi: l’onda rimane bloccata all’orizzonte degli eventi.
Ci interessa particolarmente il primo caso, in cui l’onda riesce ad arrivare su $\mathscr{I}^+$. Per l’approssimazione dell’ottica geometrica, manterrà la stessa fase durante il percorso, che è una geodetica. Per cui se la forma asintotica di $g_\omega$ su $\mathscr{I}^+$ è
$$g_{\omega}=\frac{1}{\sqrt{2\pi \omega}}\frac{1}{r}e^{-i\omega u} \,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{su}\,\,\,\,\,\mathscr{I}^+$$
Allora su $\mathscr{I}^-$ manterrà la stessa fase, ma potrà avere una normalizzazione diversa,
$$g_{\omega}=\frac{C}{\sqrt{2\pi \omega}}\frac{1}{r}e^{-i\omega u(v)} \,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{su}\,\,\,\,\,\mathscr{I}^-$$
dove $u(v)$ è il punto finale di arrivo su $\mathscr{I}^+$ per un’onda che segue una geodetica radiale nulla che parte da $v$ su $\mathscr{I}^-$. $C$ è una costante che rappresenta la nuova normalizzazione e si semplificherà nel seguito.
Dobbiamo quindi:
- Giustificare l’approssimazione dell’ottica geometrica
- Calcolare la forma della funzione $u(v)$
Un punto importante è che il contributo maggiore al calcolo viene dalle onde che passano vicino all’orizzonte degli eventi, che subiranno un forte spostamento verso il blu (cioè aumenteranno di frequenza).
Ignoreremo la possibile interazione della materia in collasso con l’onda: ciò perché le onde che hanno un grande valore di $u$ all’inizio passano molto vicino all’orizzonte degli eventi nel diagramma, e pertanto saranno fortemente spostate verso il blu (avranno cioè una frequenza molto elevata) e quindi difficilmente saranno modificate da possibili interazioni. Al contrario le onde con un piccolo valore di $u$ incontrano il corpo in collasso all’inizio del collasso quando il corpo ha densità bassa e quindi hanno bassa probabilità di interagire.
Lo stesso principio delle alte frequenze giustifica l’approssimazione dell’ottica geometrica. Infatti supponiamo in generale che un’onda $F=A e^{i\lambda S}$ soddisfi l’equazione d’onda $\nabla_\mu \nabla^\mu F = 0$. L’approssimazione è valida nel caso in cui $A$ vari molto lentamente confrontata con la fase, ovvero se la fase ha frequenze elevate (in altri termini, se $\lambda \gg 1$). Inserendo nell’equazione d’onda abbiamo
$$\begin{align*}
0 = \nabla_\mu \nabla^\mu F &= \nabla_\mu \nabla^\mu (A e^{i\lambda S})=\\
&=\nabla_\mu (e^{i\lambda S} \nabla^\mu A+F i\lambda \nabla^\mu S)=\\
&=e^{i\lambda S}\nabla_\mu \nabla^\mu A+\nabla^\mu A \nabla_\mu e^{i\lambda S}+(e^{i\lambda S} \nabla_\mu A+F i\lambda \nabla_\mu S) i\lambda \nabla^\mu S+F i\lambda\nabla_\mu \nabla^\mu S
\end{align*}$$
Poiché $\lambda \gg 1$, teniamo solo il termine principale, cioè quello in $\lambda^2$, che dà $\nabla_\mu S \nabla^\mu S=0$. Questo risultato può essere interpretato nel modo seguente: il vettore $k_\mu = \nabla_\mu S$ è il vettore normale alle superfici $S = \mathrm{costante}$. L’equazione d’onda nell’approssimazione dell’ottica geometrica ci dice che $k^\mu k_\mu = 0$, cioè che le superfici $S = \mathrm{costante}$ sono superfici nulle. In particolare $k^\mu$ sarà il vettore tangente ad una curva, e questa curva è una geodetica. Infatti
$$0=\nabla_\mu (k^\nu k_\nu) = 2 k^\nu \nabla_\mu k_\nu = 2 k^\nu \nabla_\mu \nabla_\nu S = 2 k^\nu \nabla_\nu \nabla_\mu S= 2 k^\nu \nabla_\nu k_\mu$$
dove abbiamo usato il fatto che le derivate covarianti di una funzione commutano. Per cui $k_\nu$ soddisfa l’equazione delle geodetiche. L’interpretazione di questo risultato è che nell’approssimazione dell’ottica geometrica, la superficie di fase costante di una certa onda può essere tracciata avanti o indietro nel tempo seguendo geodetiche nulle.
Ora dobbiamo ricavare la forma della funzione $u(v)$. Nell’immagine sotto osserviamo un’immagina simile alla precedente in cui abbiamo due geodetiche radiali nulle entranti che partono da $\mathscr{I}^-$, quindi con due valori distinti di $v= \mathrm{costante}$; una volta arrivate al centro del corpo in collasso diventano geodetiche radiali nulle uscenti, cioè separatamente con $u= \mathrm{costante}$:
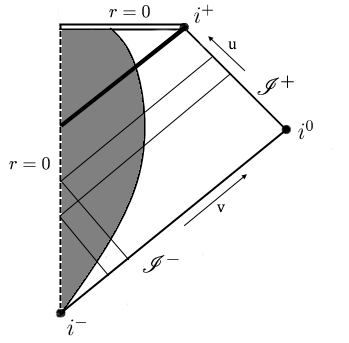
L’argomentazione di Hawking su questo punto è piuttosto difficile. Noi ne proponiamo una leggermente diversa. All’interno del corpo in collasso non ha senso usare usare le coordinate $u,v$ perché usano $r^*$ nella loro definizione, che però copre solo la parte di Schwarzschild con $2m <r <\infty$ mentre ci interessano valori di $r$ fino a zero, che in questo caso sono perfettamente validi. Quindi definiamo coordinate alternative all’interno del corpo, $u_{int} = t-r$ e $v_{int} = t+r$. Un raggio con $v=\mathrm{costante}$
Una geodetica entrante avrà abbiamo detto $v= \mathrm{costante}$; vediamo come cambia $u$. Rispetto ad un certo parametro affine $\lambda$ avremo
$$\dv{u}{\lambda} = \dv{}{\lambda}(t-r^*)=\dv{}{\lambda}(2t-v)=2\dv{t}{\lambda}=2\pqty{1-\frac{2m}{r}}^{-1} E$$
dove nell’ultimo passaggio abbiamo usato l’equazione delle geodetiche. Sempre l’equazione delle geodetiche ci dà $\dv{r}{\lambda} = -E$, ovvero $r=2m-E\lambda$ (stipulando $\lambda = 0$ quando $r=2m$), per cui sostituendo otteniamo
$$\dv{u}{\lambda}=2E -\frac{4m}{\lambda}\,\,\,\,\,\,\implies\,\,\,\,\,\, u = 2E\lambda -4m\log{\pqty{\frac{\lambda}{K_1}}}$$
In particolare sufficientemente vicino all’orizzonte
$$u \approx -4m\log{\pqty{\frac{\lambda}{K_1}}}$$
La geodetica parte da $\mathscr{I}^-$ quando il parametro affine è $\lambda = -\infty$. Se non ci fosse il corpo in collasso, raggiungerebbe $r=2m$ al parametro $\lambda = 0$ ed entrerebbe nel buco nero; tuttavia a causa della presenza del corpo in collasso, ad un certo valore negativo di $\lambda$ l’onda raggiungerà $r=0$ (che non è singolare all’interno del corpo in collasso) e diventerà un’onda uscente con $u$ costante. Tuttavia all’interno del corpo la metrica non è più Schwarzschild, per cui non possiamo porre semplicemente $r=0$; dovremmo piuttosto porre $r$ uguale al punto che nella metrica di Schwarzschild equivale ad $r=0$ nella metrica del collasso, ma ciò dipende dai dettagli del collasso. Pertanto seguiamo una strada alternativa.
Nota: l’argomentazione di questo punto è cruciale, e ironicamente non sono convinto che questa argomentazione funzioni. Ne trovate una alternativa nell’articolo originale di Hawking.
Data una geodetica con $v=v_1$, otteniamo la geodetica con $v=v_2$ per semplice traslazione del vettore $v$ di $v_2-v_1$, e la traslazione è generata dal vettore $\pdv{}{v}$, dove $K_2$ è un fattore di normalizzazione. Pertanto se la prima geodetica raggiunge $r=0$ al parametro affine $\lambda_1$, la seconda geodetica lo raggiungerà al parametro affine $\lambda_2$ in modo che $\lambda_2-\lambda_1 = K_2 (v_2-v_1)$. In particolare scegliendo $v_1=v_0$ e $v_2 = v$ abbiamo $\lambda_1 = 0$, per cui sostituendo otteniamo
$$u \approx -4m\log{\pqty{\frac{v_0-v}{K}}}$$
dove $K$ è una qualche costante positiva. Questa è la relazione che cerchiamo.
Invertendo la relazione tra $g$ ed $f$ (cioè effettuando la trasformata inversa di Fourier), otteniamo $\alpha_{\omega \omega’} \propto \int_{-\infty}^{v_0} dv\,e^{i\omega’ v} g_\omega$, cioè con più precisione
$$\alpha_{\omega \omega’} =D \int_{-\infty}^{v_0} dv\, e^{i\omega’ v}e^{-i\omega u(v)}\\
\beta_{\omega\omega’} =D \int_{-\infty}^{v_0} dv\, e^{-i\omega’ v}e^{-i\omega u(v)}$$
dove abbiamo assorbito tutte le costanti comuni in $D$. L’integrale è troppo difficile da effettuare analiticamente; pertanto ci limiteremo a massaggiarlo in modo da metterlo in forma identica sia per $\alpha$ che per $\beta$. Sostituiamo quindi $s=v_0-v$ e $s=v-v_0$ nelle formule per $\alpha$ e $\beta$ ottenendo:
$$\alpha_{\omega\omega’} =D e^{i\omega’ v_0}\int_{0}^{+\infty} ds\, e^{-i\omega’ s}\exp{\bqty{i\omega 4m\log{\pqty{\frac{s}{K}}}}}\\
\beta_{\omega \omega’} =D e^{-i\omega’ v_0}\int_{-\infty}^{0} ds\, e^{-i\omega’ s}\exp{\bqty{i\omega 4m\log{\pqty{\frac{-s}{K}}}}}$$
Ora nel primo integrale ruotiamo nel piano complesso la semiretta d’integrazione da $(0,+\infty)$ a $(0,-i\infty)$; ciò si può fare purché non ci siano singolarità nel mezzo. Sostituiamo quindi $s=is’$
$$\alpha_{\omega\omega’} =-iD e^{i\omega’ v_0}\int_{-\infty}^{0} ds’\, e^{\omega’ s’}\exp{\bqty{i\omega 4m\log{\pqty{\frac{is’}{K}}}}}\\
\beta_{\omega \omega’} =i D e^{-i\omega’ v_0}\int_{-\infty}^{0} ds’\, e^{\omega’ s’}\exp{\bqty{i\omega 4m\log{\pqty{\frac{-is’}{K}}}}}$$
dove nel secondo caso abbiamo ruotato da $(-\infty,0)$ a $(-i\infty,0)$ e sostituito $s=is’$. Per calcolare i logaritmi nel piano complesso dobbiamo scegliere un taglio; scegliamo di tagliare lungo la semiretta reale negativa $(-\infty,0)$. Dato un numero complesso $z=re^{i\theta}$ ciò corrisponde a prendere $\theta \in (-\pi,\pi)$. Ora in entrambi i casi $s'<0$, pertanto $is’=|s’| e^{-i\pi/2}$ e $-is’=|s’| e^{i\pi/2}$. Quindi
$$\log{\pqty{\frac{is’}{K}}} = \log{\pqty{\frac{|s’|}{K}}}-i\frac{\pi}{2}\\
\log{\pqty{\frac{-is’}{K}}} = \log{\pqty{\frac{|s’|}{K}}}+i\frac{\pi}{2}$$
Inserendo otteniamo:
$$\alpha_{\omega\omega’} =-iD e^{i\omega’ v_0}e^{2\pi\omega m}\int_{-\infty}^{0} ds’\, e^{\omega’ s’}\exp{\bqty{i\omega 4m\log{\pqty{\frac{|s’|}{K}}}}}\\
\beta_{\omega \omega’} =i D e^{-i\omega’ v_0} e^{-2\pi\omega m} \int_{-\infty}^{0} ds’\, e^{\omega’ s’}\exp{\bqty{i\omega 4m\log{\pqty{\frac{|s’|}{K}}}}}$$
Quindi abbiamo:
$$\frac{|\alpha_{\omega\omega’}|^2}{|\beta_{\omega\omega’}|^2}=e^{8\pi m \omega}$$
Utilizzando la formula ottenuta in precedenza dalle relazioni di commutazione,
$$\int d\omega’ \pqty{|\alpha_{\omega\omega’}|^2-|\beta_{\omega \omega’}|^2}=\delta(0)$$
otteniamo finalmente
$$\bra{0_{-}}b_\omega^\dagger b_\omega\ket{0_{-}}=\int d\omega’|\beta_{\omega \omega’}|^2=\frac{\delta(0)}{e^{8\pi m \omega}-1}$$
che è uno spettro termico alla temperatura
$$T = \frac{1}{8\pi m}$$
Il fattore $\delta(0)$ che è infinito si riferisce al fatto che il flusso di particelle continua per sempre, anche dopo che il collasso è terminato e lo spaziotempo è descritto interamente dalla metrica di Schwarzschild.
