Abbiamo già visto un semplice esempio in cui il campo gravitazionale crea delle particelle. Il punto cruciale stava nel fatto che la metrica non era stazionaria, per cui l’equazione di campo dipendeva dal tempo: pertanto in tempi diversi avevamo diverse nozioni di soluzioni a energia positiva e negativa e quindi diversi operatori di creazione e distruzione, che danno diverse nozioni di vuoto: perciò il vuoto all’inizio dell’universo non corrisponde al vuoto alla fine dell’universo.
La situazione sembra non verificarsi nella soluzione di Schwarzschild per un buco nero, che è stazionaria. In questo caso infatti la metrica non ha dipendenza temporale, e quindi la dipendenza temporale dell’equazione di campo è sempre risolta da un’onda piana uguale dappertutto. Tuttavia un buco nero reale è ottenuto dal collasso gravitazionale di materia che all’inizio dell’universo non formava un buco nero, e questo processo non è stazionario. Seguiremo il metodo originale di Hawking; esistono delle derivazioni che non fanno uso del collasso gravitazionale ma pagano il prezzo di dover introdurre condizioni ad hoc.
Considereremo lo spaziotempo con della materia sfericamente simmetrica che collassa a formare un buco nero. I dettagli della materia che collassa non ci interessano: ci basta sapere che per la simmetria sferica lo spaziotempo fuori dalla materia è descritto dalla soluzione di Schwarzschild:
$$ds^2 = \pqty{1-\frac{2m}{r}} dt^2 -\pqty{1-\frac{2m}{r}}^{-1} dr^2-r^2 d\Omega^2$$
Per visualizzare la situazione faremo uso del diagramma di Penrose per la soluzione di Schwarzschild:
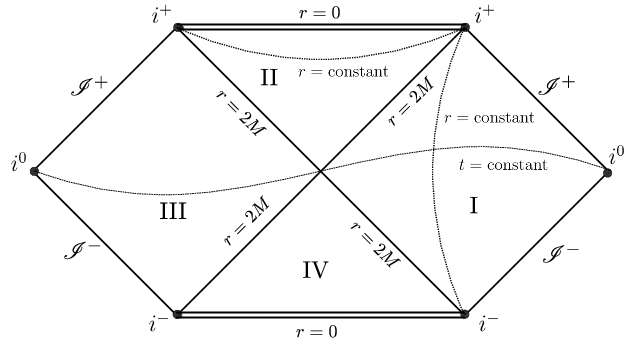
Tuttavia a noi interessa il collasso gravitazionale, che è descritto interamente dalle regioni $I$ e $II$ del diagramma, che rappresentano rispettivamente la parte fuori e dentro rispetto all’orizzonte degli eventi (mentre le regioni $III$ e $IV$ rappresentano la stessa cosa, ma per un buco bianco). La superficie della materia che collassa sarà data nel diagramma da una qualche curva che connette l’infinito temporale passato $i^-$ con un qualche punto della singolarità $r=0$:
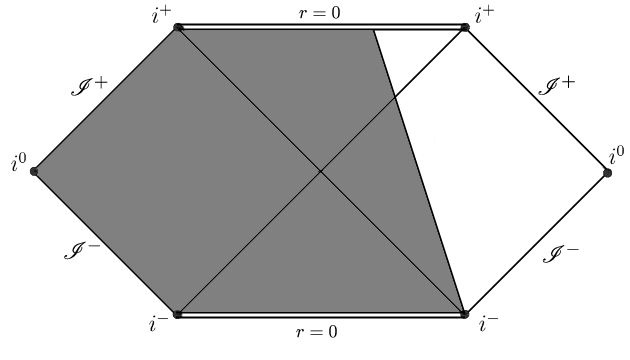
La regione ombrata a sinistra è la zona non rilevante del diagramma. Infatti le regioni $III$ e $IV$ non sono di interesse, ma anche la parte ombrata delle regioni $I$ e $II$ non è descritta dal diagramma di Schwarzschild perché la metrica all’interno della materia che collassa non è la metrica di Schwarzschild. Possiamo quindi disegnare il diagramma per lo spaziotempo del collasso:
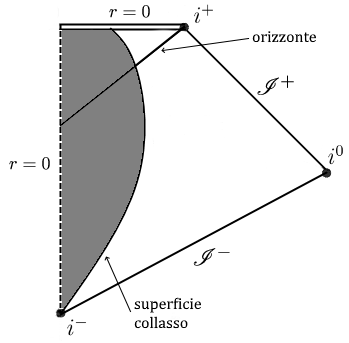
La superficie tratteggiata $r=0$ a sinistra rappresenta l’origine delle coordinate per lo spaziotempo della materia in collasso, ed è soltanto una singolarità delle coordinate.
Possiamo quindi considerare un campo scalare a massa nulla in questo spaziotempo. Poiché ha massa nulla, l’inizio dell’universo per il campo scalare è l’infinito nullo passato $\mathscr{I}^-$ e la fine dell’universo è l’infinito nullo futuro $\mathscr{I}^+$. Il campo soddisfa l’equazione di Klein-Gordon in spazi curvi $\nabla_\alpha \nabla^\alpha \phi = 0$. Ci interessa espanderlo all’inizio e alla fine e trovare una relazione tra i rispettivi operatori di creazione e distruzione. In generale possiamo espandere
$$\hat\phi(x) = \int d\omega [a_{\omega} f_{\omega}(x)+a^\dagger_{\omega} f^*_{\omega}(x)]\\
\hat\phi(x) = \int d\omega [b_{\omega} g_{\omega}(x)+b^\dagger_{\omega} g^*_{\omega}(x)+c_{\omega} h_{\omega}(x)+c^\dagger_{\omega} h^*_{\omega}(x)]$$
dove le $f, g, h$ sono un insieme di soluzioni dell’equazione d’onda con le seguenti condizioni al contorno:
- per le $f$ richiediamo che siano entranti e a energia positiva su $\mathscr{I}^-$;
- per le $g$ richiediamo che siano entranti e a energia positiva su $\mathscr{I}^+$, nonché di essere nulle sull’orizzonte;
- per le $h$ richiediamo che abbiano energia positiva sull’orizzonte e di essere nulle su $\mathscr{I}^+$.
Vediamo fra un attimo il perché della differenza. Va notato che le $f,g,h$ sono definite in linea di principio nell’intero spaziotempo e non ad esempio soltanto nelle superfici su cui abbiamo specificato le condizioni al contorno. Le $f,g,h$ sono normalizzate in modo che gli operatori di creazione e distruzione (indipendenti dal tempo) $a,b,c$ soddisfino le relazioni di commutazione canoniche
$$[a_k^\dagger,a_{k’}^\dagger]=0\,\,\,\,\,\,\,\,\,\,\,\,\,[a_k,a_{k’}]=0\,\,\,\,\,\,\,\,\,\,\,\,\,[a_k,a_{k’}^\dagger]=\delta(k-k’)$$
e le stesse per gli $b$ e per gli $c$. In termini fisici ciò rappresenta il seguente processo: un’onda ($f$) arriva da $\mathscr{I}^-$; in parte ($g$) viene sparpagliata verso $\mathscr{I}^+$ e in parte ($h$) finisce dentro l’orizzonte degli eventi. Il processo può essere visualizzato tramite il potenziale dell’equazione delle geodetiche di Schwarzschild; il problema può essere visto come un problema di sparpagliamento per un’onda quantistica in un potenziale.
Il motivo per cui dobbiamo includere le onde sull’orizzonte degli eventi è il seguente. L’equazione d’onda può essere risolta date sufficienti condizioni al contorno. Specificare dei dati su $\mathscr{I}^-$ è sufficiente a risolvere l’equazione nell’intero spaziotempo: infatti immaginiamo di disegnare in ogni punto il cono luce corrispondente. I coni avranno angoli di $45$ gradi e le direzione del moto causale (nullo o tipo tempo) è verso l’alto. Allora partendo da $\mathscr{I}^-$ e disegnando una curva che in ogni punto rimanga dentro il cono luce, possiamo raggiungere ogni punto dello spaziotempo. Si dice che $\mathscr{I}^-$ è una superficie di Cauchy. Consideriamo invece $\mathscr{I}^+$. In questo caso immaginiamo di nuovo i coni e di propagare invece le curve indietro nel tempo (ovvero nella parte sotto del cono); dal punto di vista dell’equazione differenziale, è irrilevante andare avanti o dietro, basta che si seguano delle curve causali. In questo caso riusciremo a raggiungere tutto lo spaziotempo meno la zona all’interno dell’orizzonte degli eventi. (l’orizzonte degli eventi è infatti una superficie nulla ed è uno dei limiti del cono luce su $i^+$). Perciò specificando la soluzione solo su $\mathscr{I}^+$ non siamo in grado di risolvere l’equazione d’onda su tutto lo spaziotempo; per rimediare a questo problema abbiamo specificato ulteriori condizioni al contorno sull’orizzonte degli eventi.
Ora veniamo ai dettagli. L’equazione d’onda per un tale campo nello spaziotempo di Schwarzschild è $\nabla_\alpha \nabla^\alpha \phi = 0$, ovvero
$$-\pqty{1-\frac{2m}{r}}^{-1} \partial_t^2 \phi +\frac{1}{r^2}\partial_r \bqty{\pqty{1-\frac{2m}{r}} r^2 \partial_r \phi}+\frac{1}{r^2}\Delta_{S^2} \phi=0$$
dove $\Delta_{S^2}$ è il laplaciano su una 2-sfera $S^2$. Le autofunzioni del laplaciano sferico sono le armoniche sferiche $Y_{lm}(\theta,\varphi)$, per cui scriviamo $\phi(x) = \frac{1}{r}F(t,r) Y_{lm}(\theta,\varphi)$. Il termine $1/r$ serve solo a semplificare l’equazione. Il risultato è espresso in modo elegante in termini della coordinata $r^*$ tale che $dr^* = dr/(1-2m/r)$. Otteniamo:
$$(-\partial_t^2 +\partial_{r^*}^2)F-\pqty{1-\frac{2m}{r}}\pqty{\frac{l(l+1)}{r^2}+\frac{2m}{r^3}} F=0$$
Per semplicità ci riduciamo al caso $l=0$ in cui $Y_{lm}$ è semplicemente una costante, e $\phi$ è pertanto indipendente da $\theta,\varphi$ e possiamo quindi interpretarla come un’onda sferica centrata in $0$.
In termini del tempo avanzato $v = t+r^*$ e ritardato $u = t-r^*$ l’equazione di campo diventa quindi
$$-\partial_v \partial_u F-\pqty{1-\frac{2m}{r}}\frac{2m}{r^3} F =0$$
Su $\mathscr{I}^-$ e $\mathscr{I}^+$ la coordinata $r\to \infty$ per cui l’equazione si riduce a $\partial_v \partial_u F=0$, la cui soluzione generale è $F = F_1(u)+F_2(v)$. Per definizione, su un punto di $\mathscr{I}^-$ $v$ è costante, mentre $t,r \to \infty$, quindi anche $r^* \to \infty$ e pertanto $u = v-2r^* \to -\infty$, quindi la soluzione dipende solo da $v$. In termini di onde piane, una soluzione ad energia positiva è quindi $e^{-i\omega v}$ dove $\omega$ è la frequenza dell’onda. Alla stessa maniera su un punto di $\mathscr{I}^+$ $u$ è costante e quindi un’onda piana di energia positiva è $e^{-i\omega u}$. Segue pertanto che le forme asintotiche delle onde che abbiamo definito prima sono
$$f_{\omega}=\frac{1}{\sqrt{2\pi \omega}}\frac{1}{r}e^{-i\omega v} \,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{su}\,\,\,\,\,\mathscr{I}^-\\
g_{\omega}=\frac{1}{\sqrt{2\pi \omega}}\frac{1}{r}e^{-i\omega u} \,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{su}\,\,\,\,\,\mathscr{I}^+$$
dove la normalizzazione è la stessa che nel caso di Minkowski e comunque si cancellerà alla fine, per cui non è particolarmente rilevante. Al contrario, la forma asintotica delle $h$ non ci interessa. In generale la relazione tra le $g$ e le $f$ sarà della forma
$$g_\omega =\int d\omega’ (\alpha_{\omega\omega’} f_{\omega’}+\beta_{\omega\omega’} f^*_{\omega’})$$
dove gli $\alpha, \beta$ sono dei numeri complessi. In termini di operatori di creazione e distruzione
$$b_\omega =\int d\omega’ (\alpha^*_{\omega\omega’} a_{\omega’}-\beta^*_{\omega\omega’} a^\dagger_{\omega’})$$
Pertanto se l’universo inizia nello stato di vuoto $\ket{0_{-}}$, cioè nel vuoto come è visto su $\mathscr{I}^-$, allora alla fine dell’universo, ovvero su $\mathscr{I}^+$ un’osservatore misurerà una densità di particelle
$$\bra{0_{-}}b_\omega^\dagger b_\omega\ket{0_{-}}=\int d\omega’ |\beta_{\omega\omega’}|^2$$
Pertanto restano da calcolare gli $\alpha$ e i $\beta$. Notiamo che perché siano soddisfatte le relazioni di commutazione tra gli $a$ e quelle tra i $b$, gli $\alpha, \beta$ devono soddisfare
$$\int d\omega’ \pqty{\alpha_{\omega_1 \omega’}\beta_{\omega_2 \omega’}-\alpha_{\omega_2 \omega’}\beta_{\omega_1 \omega’}}=0\\
\int d\omega’ \pqty{\alpha^*_{\omega_1 \omega’}\alpha_{\omega_2 \omega’}-\beta^*_{\omega_1 \omega’}\beta_{\omega_2 \omega’}}=\delta(\omega_1-\omega_2)$$
In particolare ponendo $\omega_1 = \omega_2 = \omega$ nella seconda equazione otteniamo
$$\int d\omega’ \pqty{|\alpha_{\omega\omega’}|^2-|\beta_{\omega \omega’}|^2}=\delta(0)$$
Abbiamo quindi una prima relazione tra $|\alpha|^2$ e $|\beta|^2$. Rimane da trovarne un’altra per completare il calcolo, cosa che faremo nel prossimo articolo.
