Il sistema per cui si verifica il cosiddetto effetto Hall è un sistema di elettroni in due dimensioni ($x,y$) soggetti ad un campo magnetico lungo $z$ e ad un campo elettrico lungo $x$. Il sistema esibisce una serie di comportamenti particolari. Questo articolo è tratto principalmente dagli appunti di David Tong.
Nel caso classico, che abbiamo già studiato nell’articolo sul modello di Drude, il sistema esibisce sia una corrente parallela al campo elettrico sia una corrente ad esso trasversale. La resistività è data da:
$$\rho = \begin{pmatrix}\frac{m}{e^2 n \tau} & B/ne\\ – B/ne & \frac{m}{e^2 n \tau}\end{pmatrix}$$
Per cui le due resistenze $\rho_{xx}$ e $\rho_{xy}$ hanno il seguente andamento in funzione del campo magnetico applicato al campione:
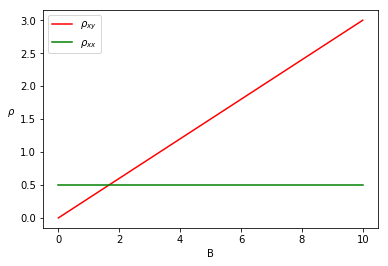Questo è l’effetto Hall classico. La corrente trasversale è poco intuitiva, ma facilmente predicibile.
L’effetto Hall quantistico
Ora se raffreddiamo il sistema di elettroni a temperature molto basse, circa $T\approx 4 \mathrm{K}$ e lo sottoponiamo a campi magnetici elevati (fino a circa $10 \mathrm{T}$) otteniamo per le due resistività un andamento molto diverso:
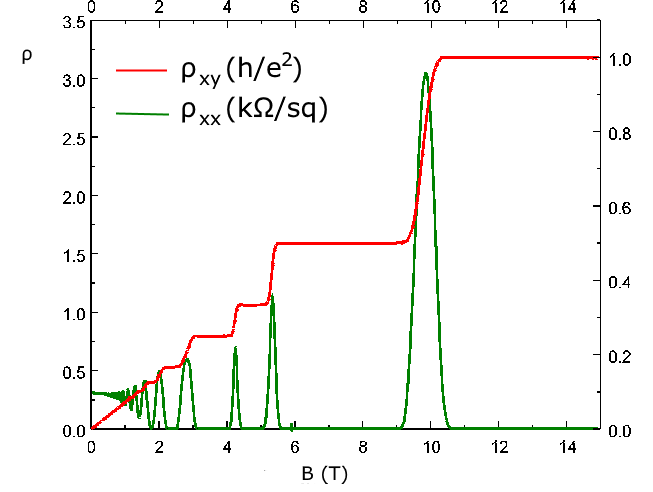
Ovvero:
- La resistività trasversale forma dei plateau sui valori $1/N$ dove $N$ è un intero
- La resistività longitudinale è nulla quando la trasversale è su un plateau, e ha un picco nella zona di transizione tra due plateau diversi.
- Per campi magnetici piccoli (circa $B<2\mathrm{T}$) il comportamento delle resistività è identico a quello classico.
Questo fenomeno, noto come effetto Hall quantistico, è un’altra manifestazione della meccanica quantistica a basse temperature. Eppure abbiamo visto che di per sé la meccanica quantistica non predice la quantizzazione della resistività. Infatti avevamo ottenuto per la resistività:
$$\rho = \frac{2\pi\hbar}{e^2}\frac{1}{N}\begin{pmatrix}0&-1\\1&0\end{pmatrix}$$
dove $N$ è il numero di livelli di Landau occupati. Ciò non implica la quantizzazione, perché $N$ non è necessariamente intero (possiamo avere ad esempio l’ultimo livello occupato a metà). Ci proponiamo di spiegare:
- perché la resistività longitudinale è quantizzata?
- perché la resistività parallela è nulla sui plateau e ha picchi nelle transizioni?
- perché il risultato quantistico fallisce per campi magnetici bassi?
Nell’analisi classica (Drude) abbiamo incluso il termine $\tau$, ovvero le collisioni casuali degli elettroni col disordine del materiale. Ignorandole, il risultato di Drude e quello quantistico sono in accordo. Pertanto l’idea è di introdurre il disordine nell’analisi quantistica, e spiegare così la quantizzazione della resistività.
Analisi quantistica col disordine
Modelliamo il disordine come un potenziale $V(x,y)$ ignoto. Su di esso imponiamo due condizioni:
- Dev’essere piccolo: $V\ll\hbar \omega_B$. In questo modo i livelli di Landau rimangono separati e non si sovrappongono.
- Deve variare lentamente: $\nabla V \ll \hbar\omega_B/l_B$ dove la lunghezza magnetica $l_B$ è la larghezza tipica di una funzione d’onda, ovvero guardando la formula per la funzione d’onda, $l_B = \sqrt{\hbar/eB}$.
Il potenziale $V$ avrà una serie di massimi e minimi. Le linee equipotenziali attorno ad un massimo o ad un minimo saranno più o meno circolari attorno al massimo/minimo, e gli elettroni si muoveranno lungo le linee equipotenziali. Pertanto gli elettroni che finiscono su un massimo/minimo rimarranno sempre attorno al massimo/minimo, come esplicato in figura:
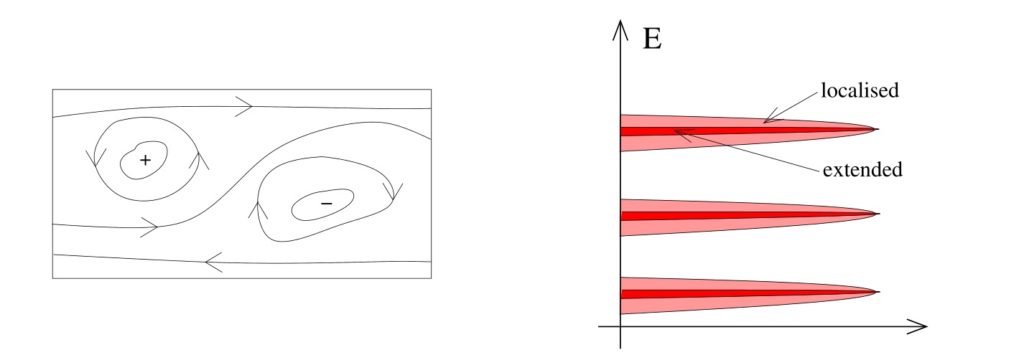
Dagli appunti di David Tong
Gli elettroni costretti ad orbitare massimi o minimi sono effettivamente bloccati, e non possono trasportare corrente da una parte all’altra del campione: questi stati sono detti localizzati. Gli altri elettroni invece possono trasportare corrente e i corrispondenti stati sono detti estesi.
Aggiungendo il potenziale $V$ i singoli livelli di Landau si allargheranno:
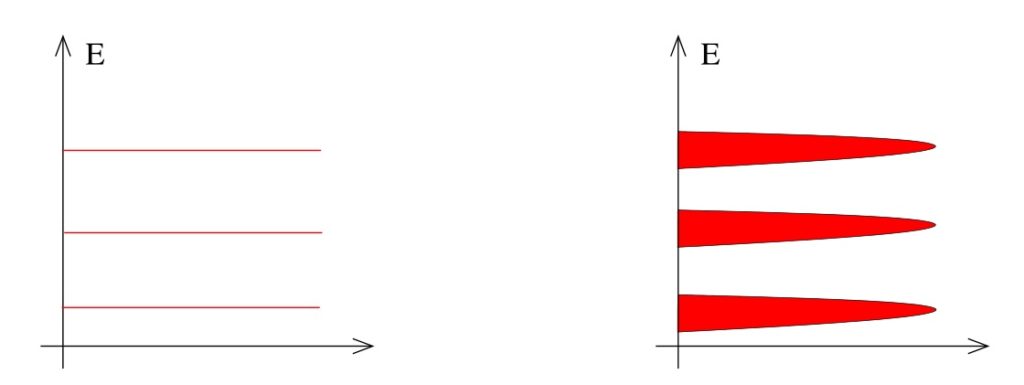
Dagli appunti di David Tong
All’interno del singolo livello, gli elettroni con energia più bassa e più alta saranno quelli vicino ai minimi e ai massimi, per cui la parte alta e bassa di un singolo livello di Landau sarà occupata dagli stati localizzati. La parte in mezzo sarà occupata dagli stati estesi, come mostrato in figura.
Questo spiega i plateau: immaginiamo infatti di aver riempito esattamente $N$ livelli di Landau. La densità elettronica $n$ è fissa, e aumentiamo lentamente $B$. Avvengono le seguenti cose:
- La degenerazione del singolo livello aumenta col campo magnetico. Per cui se $B$ aumenta i livelli di Landau sottostanti l’ultimo potranno contenere più elettroni, e il riempimento dell’ultimo livello occupato diminuirà.
- Poiché gli stati ad energia più elevata sono localizzati, i primi stati che saranno spopolati saranno stati localizzati, ma questi non trasportano corrente, per cui all’inizio la resistività rimarrà la stessa.
- Alzando ancora il campo magnetico cominciamo a spopolare gli stati estesi, per cui la resistività trasversale diminuirà: siamo ad punto di transizione.
- Una volta spopolati tutti gli stati estesi dell’$N$-esimo livello, la resistività sarà di nuovo su un plateau perché adesso spopoliamo di nuovo stati localizzati, finché l’$N$-esimo livello sarà vuoto. Allora passiamo a spopolare gli stati localizzati del livello $N-1$, ma la resistività rimane la stessa perché appunto non tocchiamo gli stati estesi.
Rimane solo un dettaglio: diminuendo il numero di stati che trasporta corrente, non dovrebbe cambiare la resistività? La formula per la resistività nel caso di disordine è la stessa di quella nel caso senza disordine, calcolata supponendo che tutti gli stati di un livello di Landau contribuissero alla corrente. In realtà no: la resistività dei livelli estesi diminuisce per compensare il minor numero di livelli che conducono corrente, facendo rimanere la formula identica. Una dimostrazione di questo fatto è possibile in un sistema modificato, ed è dovuta a Laughlin (la vedremo un’altra volta).
Abbiamo quindi spiegato il comportamento di $\rho_{xy}$. Inoltre se $B$ piccolo, allora le energie occupate sono basse e quindi il disordine è importante, per cui otteniamo la stessa cosa del caso classico con disordine (che è d’altronde in accordo col caso quantistico). In altri termini, tutti i livelli di Landau occupati sono compenetrati l’uno nell’altro.
Il comportamento della resistività longitudinale
Ci aspettiamo dai calcoli che $\rho_{xx}$ sia sempre nullo; in caso di presenza di disordine, magari non nullo ma comunque molto piccolo. La domanda è: perché forma un picco nelle zone di transizione? Prima di tutto bisogna considerare che nel grafico i picchi di $\rho_{xx}$ sono esagerati: infatti $h/e^2 \approx 26 \mathrm{k\Omega}$, mentre appunto $\rho_{xx} \approx \mathrm{k\Omega}$. Per questo motivo la conducibilità termica rimane molto piccola. Ad esempio per il picco più grande abbiamo $\sigma_{xx}=\rho_{xx}/(\rho_{xx}^2+\rho_{xy}^2) \approx 4 \times 10^{-6} \mathrm{\Omega}^{-1}$, valore tipico degli isolanti.
La resistività è una misura di dissipazione. Il motivo dei picchi è che nelle fasi di transizione da un plateau all’altro il disordine è più accentuato. Questo perché nella fase di transizione non c’è un divario energetico tra l’ultimo stato occupato e il successivo disponibile (sono entrambi stati estesi). Perciò il disordine, che causa sparpagliamento (scattering), può sparpagliare gli elettroni in un gran numero di stati diversi, aumentando la dissipazione. Ciò non è invece possibile quando tutti gli stati estesi sono occupati: in tal caso c’è un divario energetico e gli elettroni non possono andare da nessuna parte. L’altezza dei picchi cresce con $B$ perché aumenta anche la degenerazione, e quindi gli elettroni hanno più stati dove sparpagliarsi.