Un cunicolo spaziotemporale (in inglese wormhole) è un ipotetico “buco” che connette due diversi universi (figura a) oppure due parti dello stesso universo (figura b).
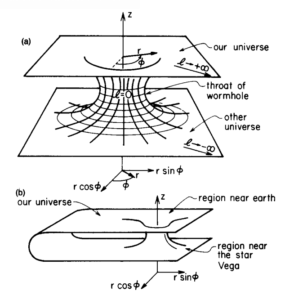
Esempi di cunicoli spaziotemporali. Immagine presa da Morris & Thorne (1988).
Sono oggetti di particolare interesse perché permetterebbero di raggiungere luoghi estremamente lontani aggirando il limite della velocità della luce. Per questo sono spesso adottati come soluzione al problema dei viaggi interstellari nelle opere di fantascienza. Le equazioni di Einstein ammettono diverse soluzioni semplici che rappresentano cunicoli spaziotemporali almeno in teoria attraversabili; il problema è che per realizzare uno di questi oggetti serve materia esotica, ovvero materia con densità di energia negativa: non si conosce niente con proprietà del genere e non è chiaro se sia realizzabile.
Un caso particolarmente semplice è quello dello spaziotempo di Schwarzschild. Partendo dalla metrica
$$ds^2 = -\left(1-\frac{2M}{r}\right) dt^2 + \frac{dr^2}{1-\frac{2M}{r}} + r^2 (d\theta^2+ \sin^2{\theta}\,d\phi^2)$$
Possiamo effettuare una trasformazione di coordinate introducendo una coordinata $\rho$ tale che
$$r = \rho + M + \frac{M^2}{4\rho}$$
La metrica diventa:
$$ds^2 = -\pqty{\frac{1-M/2\rho}{1+M/2\rho}}^2 dt^2 + \pqty{1+\frac{M}{2\rho}}^4\bqty{d\rho^2 + \rho^2 (d\theta^2+ \sin^2{\theta}\,d\phi^2)}$$
Tuttavia la funzione che definisce $r$ non è iniettiva:
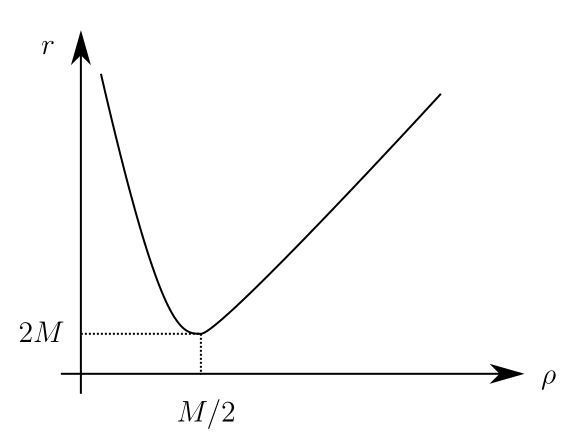
Pertanto ad ogni valore di $r$ corrispondono due valori di $\rho$. Possiamo di certo limitarci ai due casi $0 < \rho < M/2$ ed $\rho> M/2$, tuttavia possiamo dimenticarci dell’esistenza della coordinata $r$ e semplicemente considerare un nuovo spaziotempo in cui $\rho > 0$ (questa procedura è detta estensione analitica). L’unico problema è la singolarità delle coordinate in $\rho = M/2$, che corrisponde alla singolarità in $r=2M$, ma non è un problema grave perché la singolarità è un artificio delle coordinate. Entrambe le regioni $0 < \rho < M/2$ ed $\rho> M/2$ corrispondono a $r>2M$, cioè sono regioni all’esterno del buco nero.
Se consideriamo una fetta $t = \mathrm{costante}$ del nuovo spaziotempo, la metrica è data da
$$ds^2 = \pqty{1+\frac{M}{2\rho}}^4\bqty{d\rho^2 + \rho^2 (d\theta^2+ \sin^2{\theta}\,d\phi^2)}$$
In questo caso la singolarità non c’è e lo spazio è definito per tutto $\rho > 0$. Lo spazio è topologicamente $\mathbb{R} \times S^2$. Possiamo visualizzarlo sopprimendo la coordinata $\theta$, ottenendo:
$$ds^2 = \pqty{1+\frac{M}{2\rho}}^4\pqty{d\rho^2 + \rho^2 d\phi^2}$$
La metrica è quella di un cilindro con raggio variabile. Nel caso $\rho \to 0$ oppure $\rho \to \infty$ la metrica è semplicemente la metrica di uno spazio piatto.
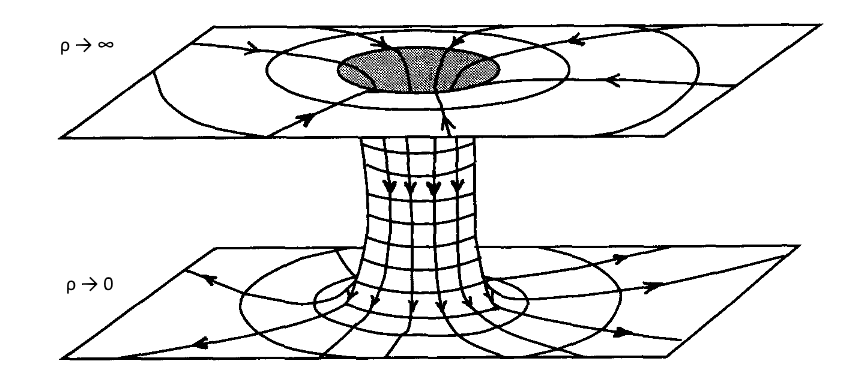
o anche:
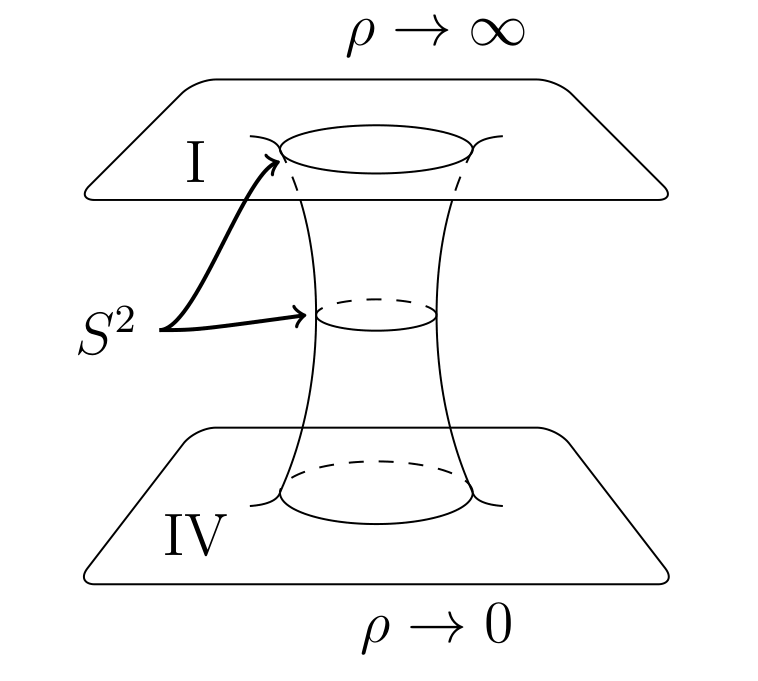
L’oggetto nel disegno è un cunicolo spaziotemporale che connette due regioni piatte di uno spaziotempo, ed è detto ponte di Einstein-Rosen. Va notato che la topologia della gola del cunicolo è quella di un cerchio solo perché abbiamo soppresso la coordinata $\theta$. Rimettendola otteniamo la topologia di una sfera.
