Consideriamo un sistema di $N$ spin, ognuno dei quali può assumere due possibili energie: $+\mu$ o $-\mu$. Lavoriamo nell’insieme microcanonico, per cui l’energia è data e la temperatura dev’essere calcolata. Se lavorassimo nell’insieme canonico staremmo già presupponendo l’equilibrio termico con un serbatoio esterno, ma così staremmo già partendo con una temperatura negativa.
Chiamiamo $N_{\uparrow}$ ed $N_{\downarrow}$ il numero di stati spin su e giù rispettivamente. Abbiamo $N_\uparrow +N_\downarrow=N$. L’energia del sistema è data da:
$$E = \mu N_\uparrow -\mu N_\downarrow = \mu (N-2N_\downarrow)$$
L’entropia è data dal logaritmo dei possibili modi per ottenere una configurazione con un certo $N_\downarrow$:
$$S = k \log{\Omega(E)} = k \log{{N \choose N_\downarrow} }$$
Usando la formula di Stirling otteniamo:
\begin{align*}
S &= k\bqty{ N \log{N} -N-N_\downarrow \log{N_\downarrow}+N_\downarrow -(N-N_\downarrow) \log{(N-N_\downarrow)} +(N-N_\downarrow)-1}=\\
&=k\bqty{ N \log{N}-N_\downarrow \log{N_\downarrow} -(N-N_\downarrow) \log{(N-N_\downarrow)}-1}
\end{align*}
Pertanto la derivata dell’entropia rispetto a $N_\downarrow$ è:
$$\dv{S}{N_\downarrow} = k\log{\pqty{\frac{N}{N_\downarrow}-1}}$$
Invertendo la relazione sopra possiamo esprimere tutto in termini dell’energia:
$$N_\downarrow = \frac{1}{2}\bqty{N-\frac{E}{\mu}}$$
Quindi otteniamo:
$$\dv{S}{N_\downarrow} = -k\log{\pqty{\frac{E_{\mathrm{max}}-E}{E_{\mathrm{max}}+E}}}$$
dove $E_{\mathrm{max}} = N \mu$. Per definizione, la temperatura è:
$$\frac{1}{T} \equiv \dv{S}{E} = \dv{N_\downarrow}{E}\dv{S}{N_\downarrow}= \frac{k}{2\mu}\log{\pqty{\frac{E_{\mathrm{max}}-E}{E_{\mathrm{max}}+E}}}$$
dove $-E_{\mathrm{max}}\leq E\leq E_{\mathrm{max}}$. Il grafico è il seguente:
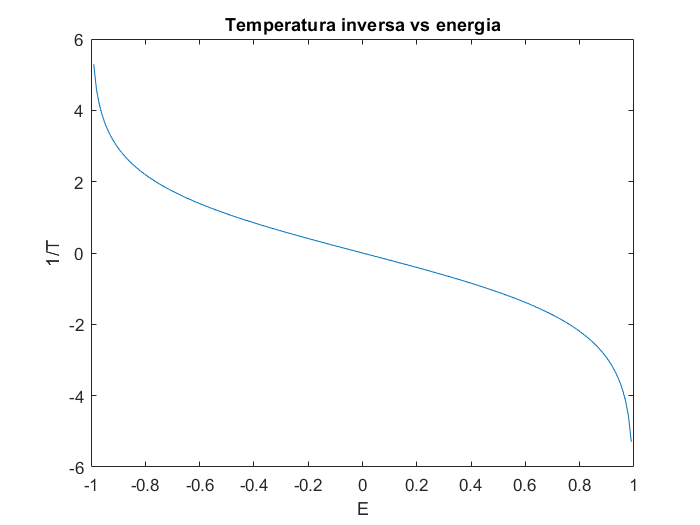
Notiamo che
$$\frac{1}{T} \geq 0 \iff E \leq 0$$
Pertanto partendo da uno stato con $T > 0$ e fornendo energia è possibile prima raggiungere lo stato ad infinita temperatura $1/T=0$ e aumentando ancora l’energia, stati a temperatura negativa. Questi hanno un comportamento peculiare: aumentandone l’energia, l’entropia decresce. In laboratorio, è possibile realizzare stati a temperatura negativa partendo da uno a temperatura positiva e capovolgendo tutti gli spin istantaneamente.
