Abbiamo visto come usare l’espansione viriale per calcolare le correzioni alla legge dei gas perfetti nel caso di interazioni tra le particelle. Tuttavia abbiamo soltanto calcolato la prima correzione (il secondo coefficiente viriale), rimandando il resto. In questo articolo vediamo come calcolare le correzioni a tutti gli ordini.
Per l’impostazione generale rimando all’articolo precedente. Vogliamo calcolare la funzione di partizione canonica per $N$ particelle:
$$Z_N =\frac{1}{N! h^{3N}} \int \prod_{i=1}^N d^3 x_i\, d^3 p_i \, e^{-\beta \bqty{\sum_{i}^N\frac{p_i^2}{2m}+\sum_{j<k} U(r_{jk})}}$$
dove $r_{jk}=|\mathbf{x}_j -\mathbf{x}_k|$. Possiamo subito integrare gli impulsi con la solita formula gaussiana, ottenendo:
$$Z_N =\frac{1}{N! \lambda^{3N}} \int \prod_{i=1}^N d^3 x_i\, e^{-\beta \sum_{j<k} U(r_{jk})}$$
dove $\lambda$ è la lunghezza d’onda termica. Potremmo pensare di espandere l’esponenziale in serie di Taylor, ma non è vero che è sempre piccolo: infatti per $r \to 0$ tipicamente $U \to \infty$, il che rende l’espansione inutile. Definiamo invece la funzione f di Mayer:
$$f_{ij}=f(r_{ij}) = e^{-\beta U(r_{ij})}-1$$
Abbiamo già visto che il secondo coefficiente viriale può essere espresso in termini di $f$, e vediamo che si comporta meglio come parametro di espansione: quando $U$ è piccolo, allora $f$ è circa $U$, mentre per $U$ grande $f$ tende a $-1$. In termini di $f$,
$$Z_N =\frac{1}{N! \lambda^{3N}} \int \prod_{i=1}^N d^3 x_i\, \prod_{j<k} \pqty{1+f_{jk}}=\frac{1}{N! \lambda^{3N}} \int \prod_{i=1}^N d^3 x_i\, \pqty{1+\sum_{j<k} f_{jk}+\sum_{j<k,\, l<m} f_{jk}f_{lm} + \cdots}$$
Il primo termine è semplicemente $V^N$, mentre il secondo termine dà la formula per il secondo coefficiente viriale.
I vari termini da integrare sono tutti della forma $f_{jk}f_{lm}\ldots$ per cui rappresentiamo ognuno di questi con un grafo, secondo le seguenti regole:
- Disegniamo $N$ punti, uno per ogni particella
- Se il termine da integrare contiene $f_{ij}$ disegniamo una linea tra l’atomo $i$ e l’atomo $j$.
Per $N = 4$ alcuni dei grafi sono i seguenti:
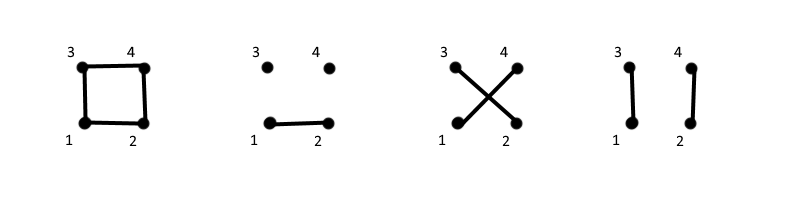
corrispondenti rispettivamente ai termini $f_{12} f_{13}f_{24}f_{34}$, poi $f_{12}$, poi $f_{14}f_{23}$ e $f_{13}f_{24}$. Notiamo che gli ultimi due sono formati da due componenti disconnessi.
Nelle applicazioni $N$ è enorme, ma non avremo in realtà bisogno di disegnare tutte le $N$ particelle. Notiamo che ogni possibile grafo è contenuto esattamente una volta nell’espansione della funzione di partizione, per cui:
$$Z_N =\frac{1}{N! \lambda^{3N}} \sum_{G} W[G]$$
dove gli $G$ rappresentano i possibili grafi e $W[G]$ è l’integrale sul grafo, cioè ad esempio per $N=4$ dato il grafo $G=$
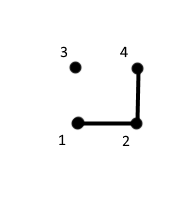
questo corrisponde a $f_{12}f_{24}$ per cui $W[G] = \int \prod_{i=1}^N d^3 x_i\, f_{12} f_{24}$.
Notiamo che se il grafo è formato da due sottografi disconessi, come ad esempio nel caso seguente:
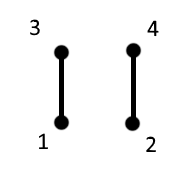
allora l’integrale $W[G]$ fattorizza nel prodotto degli integrali sui due sottografi:
$$W[G] =\pqty{\int \prod_{i \neq 1,2,3,4}^N d^3 x_i\,} \pqty{\int d^3 x_1\, d^3 x_3 \, f_{13}}\pqty{\int d^3 x_2\, d^3 x_4\, f_{24}}$$
Dato un grafo, chiamiamo i suoi diversi componenti connessi grappoli (“cluster” in inglese). Un $l-$grappolo è un grappolo formato da $l$ particelle, cioè da $l$ punti. Dato un grafo $G$ chiamiamo $m_l$ il numero di $l-$grappoli di $G$. I numeri $m_l$ soddisfano la condizione $\sum_{l=1}^N m_l l = N$. L’idea è organizzare l’espansione di $Z_N$ per grappoli, in modo tale che gli $l$-grappoli contribuiscano di più degli $(l+1)-$grappoli.
Chiamiamo $U_l$ l’integrale su tutti gli $l-$grappoli. Gli $l$-grappoli sono in pratica i grafi connessi con $l$ punti:
$$U_l =\int \prod_{i=1}^l d^3 x_i \sum_{G \in l-\mathrm{grappoli}} G$$
Adesso scegliamo una serie di numeri $m_l$ che soddisfino la condizione $\sum_{l=1}^N m_l l = N$, ad esempio $N=5$ con $m_1 = 0, m_2 = 1, m_3 = 1, m_4 = m_5 = 0$. Abbiamo
$ U_2 = \int d^3 x_1\, d^3 x_2 ($ ![]() $)$
$)$
$U_3 = \int d^3 x_1\, d^3 x_2\,d^3 x_3\,($ ![]() $+$
$+$ ![]() $+$
$+$ ![]() $+$
$+$ ![]() $)$
$)$
Per cui nel caso $N=5$ tutti i grafi con $m_1 = 0, m_2 = 1, m_3 = 1, m_4 = m_5 = 0$ sono dati dal prodotto
$U_2 U_3 = \int \prod_{i=1}^5 d^3 x_i ($ 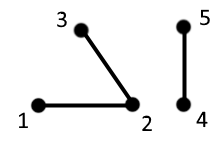 $+$
$+$ ![]() $+$
$+$ ![]() $+$
$+$ ![]() $)$
$)$
più tutte le possibili permutazioni. Quante sono le permutazioni? Possiamo permutare tutte le $N$ particelle, quindi avremo un $N!$ al numeratore. All’interno dello stesso grappolo possiamo scambiare tutte le particelle senza conseguenza, quindi dividiamo per $\prod_{l=1}^N (l!)^{m_l}$. Inoltre se abbiamo più grappoli della stessa dimensione non possiamo distinguerli, per cui mettiamo anche $\prod_{l=1}^N m_l!$ al denominatore. Infine, data una certa scomposizione $\{m_l\}$ il contributo integrale sarà dato da $\prod_{l=1}^N U_l^{m_l}$. Mettendo insieme abbiamo quindi
$$\sum_{G} W[G] =N! \sum_{\{m_l\}^\prime} \prod_{l} \frac{1}{m_l!} \pqty{\frac{U_l}{l!}}^{m_l}$$
dove la somma su $\{m_l\}^\prime$ indica la somma su tutte le possibili scelte dei numeri $m_l$ che soddisfano $\sum_{l=1}^N m_l l = N$.
Possiamo quindi inserire il risultato nella funzione di partizione grancanonica:
$$\mathcal{Z} = \sum_{N=0}^\infty \pqty{\frac{z}{\lambda^3}}^N \sum_{\{m_l\}^\prime} \prod_{l} \frac{1}{m_l!} \pqty{\frac{U_l}{l!}}^{m_l}=\\
=\sum_{N=0}^\infty \sum_{\{m_l\}^\prime} \prod_{l} \pqty{\frac{z}{\lambda^3}}^{l m_l} \frac{1}{m_l!} \pqty{\frac{U_l}{l!}}^{m_l}$$
Poiché stiamo sommando su tutti i possibili $N$, invece di sommare prima sulle configurazioni che soddisfano $\sum_{l=1}^N m_l l = N$ e poi sommare su $N$ possiamo direttamente sommare su tutte le possibili configurazioni senza restrizione. Denotiamo con $\{m_l\}$ tutte le configurazioni senza restrizione. Allora
$$\mathcal{Z}=\sum_{\{m_l\}} \prod_{l} \frac{1}{m_l!} \pqty{\frac{U_l}{l!}\frac{z^l}{\lambda^{3l}}}^{m_l}=\prod_{l} \sum_{m_l=0}^\infty \frac{1}{m_l!} \pqty{\frac{U_l}{l!}\frac{z^l}{\lambda^{3l}}}^{m_l}=\\
=\prod_{l} \exp{\pqty{\frac{U_l}{l!}\frac{z^l}{\lambda^{3l}}}}=\exp{\pqty{\frac{V}{\lambda^3}\sum_{l=1}^\infty b_l z^l}}$$
dove abbiamo definito $b_l = \frac{\lambda^3}{V} \frac{U_l}{l! \lambda^{3l}}$. Lo scambio tra produttoria e somma segue dal seguente esempio in due dimensioni, facilmente estendibile:
$$\sum_{\{m_1,\,m_2\}} f_1(m_1)f_2(m_2) = \sum_{m_1=0}^\infty \sum_{m_2=0}^\infty f_1(m_1)f_2(m_2)=\sum_{m_1=0}^\infty f_1(m_1) \sum_{m_2=0}^\infty f_2(m_2)=\prod_{l=1}^2 \sum_{m_l=0}^\infty f_l(m_l)$$
Otteniamo quindi
$$\frac{pV}{N k_B T} = \frac{\sum_{l=1}b_l z^l}{\sum_{l=1}^\infty l b_l z^l}\\
\frac{N}{V} = \frac{1}{\lambda^3} \sum_{l=1}^\infty l b_l z^l$$
A questo punto definiamo i coefficienti viriali $B_n$ in modo che
$$\frac{pV}{N k_B T} = 1 + B_2 \frac{N}{V}+ B_3 \pqty{\frac{N}{V}}^2 + \cdots$$
I coefficienti $B_n$ possono essere ottenuti nel modo seguente. Eguagliamo le due espressioni per $pV / Nk_B T$ e sostituiamo l’espressione per $N/V$. Otteniamo:
$$\sum_{l=1}^\infty b_l z^l = \sum_{l=1}^\infty l b_l z^l \sum_{n=1}^\infty B_n \pqty{\frac{1}{\lambda^3} \sum_{k=1}^\infty l b_k z^k}^{n-1}$$
Quindi moltiplichiamo i vari termini ed eguagliamo le due serie in $z$, così ottenendo i $B_n$ in termini dei $b_l$. Ad esempio per il terzo coefficiente viriale otteniamo:
$$B_3 = \lambda^6 (4 b_2^2-2b_3) =\frac{1}{V^2} \pqty{U_2}^2-\frac{1}{3V} U_3 = 4 \pqty{B_2}^2 -\frac{1}{3V} U_3$$
e così via. Gli $b_2$ sono ottenuti dagli integrali per gli $U_l$, di solito calcolati numericamente.
