La cupola di Norton è un esempio di indeterminismo in meccanica classica. L’esperimento mentale è il seguente: una pallina viene posta in cima ad una cupola di una forma specifica, appunto la cupola di Norton. Anche prescrivendo le necessarie condizioni al contorno, le equazioni di Newton non hanno una soluzione unica, invece la pallina può cominciare a scendere in un qualsiasi momento temporale completamente casuale, che non può essere determinato.
In pratica, ovviamente, anche se la pallina fosse perfettamente stabile in cima prima o poi una qualche perturbazione a caso la farebbe cadere. Tuttavia non è questo lo scopo dell’esperimento, quanto piuttosto la dimostrazione matematica che se le equazioni di Newtown sono valide, anche nella situazione ideale in cui la pallina è perfettamente bilanciata e non ci sono perturbazioni allora la pallina può comunque cominciare a cadere in un qualsiasi momento indeterminato.
Mentre si dice spesso che la meccanica quantistica non è deterministica, mentre la meccanica classica lo è, l’esperimento mentale mostra che anche le equazioni di Newton possono essere non deterministiche. Nelle prossime sezioni vediamo meglio la cupola e la spiegazione matematica del fenomeno.
La cupola di Norton
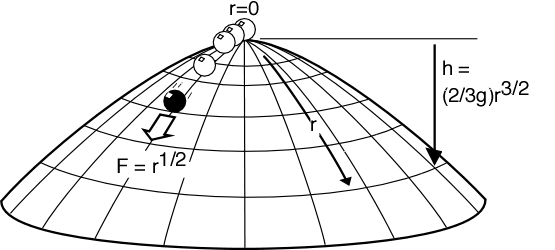
La cupola di Norton è in linea di principio costruibile in pratica, ed è come nella figura seguente:
La figura mostra una biglia in cima alla cupola, la cui forma è data dall’equazione:
$$h(r) = -\frac{2k}{3g}r^{3/2}$$
dove $r$ non è il raggio usuale ma la lunghezza d’arco, come indicato in figura. La costante $k$ è presente per motivi dimensionali. L’equazione è da considerarsi valida per $r$ sufficientemente piccolo, perché per definizione di $r$ abbiamo $\abs{h(r)} \leq r$, ma ciò non è vero per $r$ sufficientemente grande; in altri termini ad un certo punto dobbiamo troncare la cupola, ma ciò non è un problema. La biglia ruota senza scivolare e all’inizio si trova in cima alla cupola ed è immobile, cioè $r(0)=\dot r(0)=0$.
L’unica forza che agisce sulla biglia è la gravità, il cui potenziale è $m g h(r)$. L’equazione del moto è quindi:
$$m \ddot r = -\pdv{(mgh(r))}{r}\implies \ddot r = k \sqrt{r}$$
Quest’equazione ammette due possibili soluzioni che rispettano tanto l’equazione quanto le condizioni al contorno, ovvero:
$$r(t) = 0 \,\,\,\,\,\mathrm{oppure}\,\,\,\,\, r(t)=\frac{k}{144}t^4$$
e ciò è facilmente dimostrabile calcolando la soluzione esplicitamente. Possiamo anche combinare le due soluzioni per ottenerne una ancora più strana:
$$r(t) = \begin{cases}0 & t < T\\ \frac{k}{144}(t-T)^4 & t > T\end{cases}$$
dove $T$ è del tutto arbitrario. Ovvero la pallina rimane ferma per un tempo arbitrario e impredicibile, e poi comincia a muoversi. E tutto ciò in assenza di perturbazioni di qualsiasi tipo. In altre parole le equazioni di Newton non sono in grado di predire per quanto tempo la pallina rimarrà ferma in cima.
La spiegazione matematica
La spiegazione matematica di questo comportamento paradossale ha a che fare con le complicate condizioni necessarie perché un’equazione differenziale abbia soluzione unica.
Infatt l’equazione di Newton $F=ma$ è un’equazione differenziale ordinaria del second’ordine, e può essere quindi espressa come un sistema di due equazioni differenziali ordinarie del prim’ordine:
$$\begin{cases} \dot{x}(t) = v(x) \\ \dot{v}(t) = F(x,t)/m \end{cases}$$
Ponendo $\textbf{x} = (x,v)$ e $\textbf{G}=(v, F/m)$, possiamo esprimere il sistema in termini vettoriali:
$$\frac{d\textbf{x}(t)}{d t} = \textbf{G}(t, \mathbf x(t))\tag{*}$$
Il teorema matematico che ci dà le condizioni di esistenza e unicità per una soluzione di questo equazione è il seguente:
Teorema. (Picard-Lindelof) Sia $S$ la palla chiusa di raggio $R$ centrata in $\textbf{x}_0 \in \mathbb{R}^n$ e sia $t_0 \in [a,b]$. Sia inoltre $\textbf{G}: [a,b] \times S \to \mathbb{R}^n$ una funzione Lipschitziana, cioè tale che $\lVert \textbf{G}(t,\textbf{x}) -\textbf{G}(t,\textbf{y}) \lVert \leq K \lVert \textbf{x} -\textbf{y} \lVert$ per ogni $t$, $\textbf{x}$, $\textbf{y}$, dove $K$ è costante. Allora:
- Localmente esiste ed è unica la soluzione dell’equazione differenziale $(*)$ con condizione al contorno $\textbf{x}(t_0) = \textbf{x}_0$.
- Se inoltre $\sup_{[a,b]\times S} \lVert \textbf{G} \lVert \leq R/(b-a)$, allora la soluzione esiste ed è unica globalmente.
Ora se $\mathbf G$ è lipschitziana allora è anche continua, ma non viceversa. Se rilassiamo questa condizione richiedendo che $\mathbf G$ sia continua ma non necessariamente lipschitziana allora possiamo ancora dimostrare l’esistenza, ma non l’unicità. Pertanto scegliendo una qualche forza $F$ tale che $\mathbf G$ sia continua ma non lipschitziana possiamo ottenere un sistema di fisica classica che ammette più soluzioni. Questo è esattamente ciò che succede nel caso della cupola di Norton.
In questo senso l’affermazione secondo cui la fisica newtoniana è deterministica va presa con le pinze: ciò è vero solo se le forze fisiche che consideriamo soddisfano certe proprietà matematiche, che peraltro non hanno nessun ovvio significato fisico..