Abbiamo già discusso della fionda gravitazionale in un precedente articolo, limitandoci al caso in cui la velocità del pianeta e della navicella siano parallele al momento dell’approccio. Qui trattiamo il caso generale, in cui la navicella incontra il pianeta con un angolo qualsiasi.
Abbiamo visto che possiamo trattare la fionda come un urto elastico, ma includendo un angolo non funziona più: stavolta abbiamo quattro incognite (le due componenti delle velocità finali del pianeta e della navicella) ma solo tre equazioni (due dalla conservazione dell’impulso, e una dalla conservazione dell’energia). Ci servirebbe un’ulteriore condizione, ma non è chiaro quale possa essere.
Per risolvere il problema pensiamo meglio a come avviene l’approccio. Mettendoci nel sistema di riferimento del pianeta e ignorando l’attrazione del Sole, l’orbita è aperta, per cui è un’iperbole. Questa è un’approssimazione, ma è abbastanza buona: vicino al pianeta, la gravità planetaria è dominante su quella del Sole. D’altronde un’iperbole ci mette molto poco ad avvicinarsi notevolmente ai suoi asintoti, per cui l’errore che commettiamo nell’allungare “all’infinito” la sfera d’influenza gravitazionale del pianeta è piccolo.
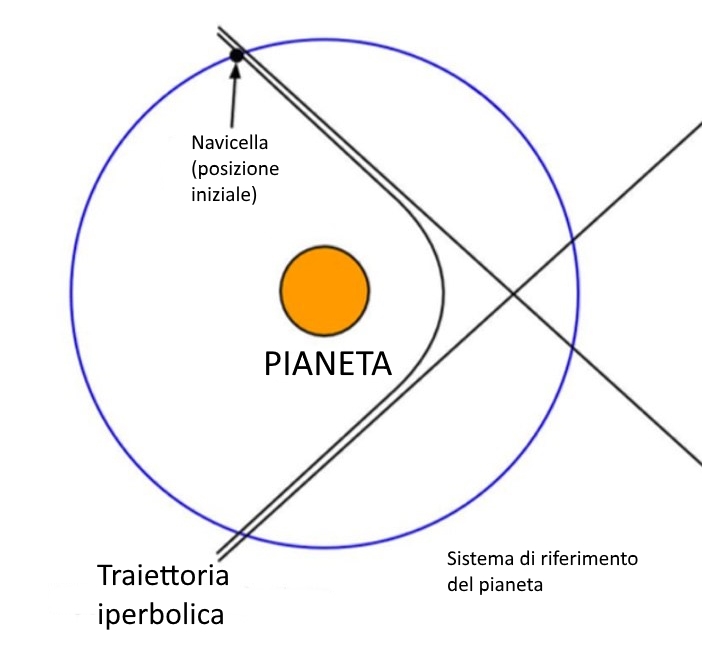
Nel sistema di riferimento del pianeta, la navicella descrive una traiettoria iperbolica.
Possiamo fare i calcoli seguendo l’articolo di R.C. Johnson, The slingshot effect. Per la simmetria dell’iperbole e la conservazione dell’energia la velocità finale della navicella sarà uguale in modulo alla velocità iniziale, ma ruotata di un certo angolo. Utilizziamo la seguente notazione:
- $\mathbf{v}_i$ e $\mathbf{v}_f$ sono le velocità iniziale e finale della navicella rispetto al Sole.
- $\mathbf{u}_i$ e $\mathbf{u}_f$ sono le velocità iniziale e finale della navicella rispetto al pianeta.
- $\mathbf V$ è la velocità del pianeta (rispetto al Sole). Supporremo che $\mathbf V$ sia identica prima e dopo l’urto: possiamo supporlo, a differenza di prima, perché non utilizzeremo le masse nei calcoli seguenti.
Per le definizioni date abbiamo:
$$\mathbf{u}_i = \mathbf{v}_i-\mathbf V\,\,\,\,\,\,\,\,\,\,\,\,\mathbf{u}_f = \mathbf{v}_f-\mathbf V$$
Inoltre, come abbiamo detto prima, nel sistema di riferimento del pianeta l’orbita della navicella è approssimabile ad un’iperbole, per cui il valore assoluto della velocità prima e dopo l’approccio non cambia: $\abs{\mathbf{u}_i} = \abs{\mathbf{u}_f}$. Ora chiamiamo:
- $\alpha_i$ l’angolo tra $\mathbf{v}_i$ e $\mathbf V$
- $\alpha_f$ l’angolo tra $\mathbf{v}_f$ e $\mathbf V$
- $\beta$ l’angolo tra $\mathbf{u}_i$ e $\mathbf{u}_f$, cioè l’angolo di deflessione dell’iperbole.
Scegliamo degli assi per cui $\mathbf V = (V,0)$. Pertanto $\mathbf{v}_i = (v_i \cos{\alpha_i}, v_i \sin{\alpha_i})$ e quindi $\mathbf{u}_i =\mathbf{v}_i-\mathbf V = (v_i \cos{\alpha_i}-V, v_i \sin{\alpha_i})$. A questo punto $\mathbf{u}_f$ è $\mathbf{u}_i$ ruotato di $-\beta$:
$$\mathbf{u}_f = (v_i \cos{\pqty{\alpha_i-\beta}}-V\cos{\beta}, v_i \sin{\pqty{\alpha_i-\beta}}+V\sin{\beta})$$
Quindi utilizzando $\mathbf{v}_f = \mathbf{u}_f + \mathbf V$ otteniamo per i componenti di $\mathbf{v}_f$:
$$\begin{cases}v_f \cos{\alpha_f} = V ( 1-\cos{\beta}) +v_i\cos{\pqty{\alpha_i-\beta}}\\ v_f \sin{\alpha_f} = V \sin{\beta} +v_i\sin{\pqty{\alpha_i-\beta}}\end{cases}\tag{1}$$
Per cui calcolando il rapporto tra le due equazioni otteniamo $\alpha_f$, mentre invece prendendo il quadrato e sommando otteniamo $v_f$. Resta solo da determinare l’angolo di deflessione $\beta$. Sappiamo che l’iperbole è data da:
$$r(\theta) = \frac{h^2/GM}{1+e\cos{\theta}}$$
dove $h$ è il momento angolare per unità di massa e $e>1$ l’eccentricità dell’orbita. Sappiamo che $r\to\pm\infty$ quando $\theta \to \pm \arccos{(1/e)}$ per cui
$$\beta = 2\arccos{(1/e)}-\pi$$
Resta quindi da determinare l’eccentricità, che è data dalla formula:
$$e=\sqrt{1+\frac{2Eh^2}{m G^2 M^2}}$$
All’infinito l’energia è data da $E = 1/2 m u_i^2$ e il momento angolare è $h=b u_i$ dove $b$ è il cosiddetto parametro d’impatto, ovvero la distanza minima di approccio nel caso in cui il pianeta abbia massa nulla. $b$ è un parametro che dipende solo dall’orbita precedente della navicella. Per cui
$$\beta=2\arccos{\pqty{1+\frac{b^2 u_i^4}{G^2 M^2}}^{-1/2}}-\pi\tag{2}$$
Per verificare la correttezza dei calcoli verifichiamo che riportino con il caso precedente, in cui $\alpha = 0$ e $b=0$. Otteniamo quindi $\beta = -\pi$ e le due equazioni sopra diventano:
$$\begin{cases}
v_f \cos{\alpha_f} = 2V -v_i\\
v_f \sin{\alpha_f} =0 \end{cases}$$
per cui $\alpha_f=0$ e $v_f = 2V-v_i$ come ci aspettavamo.
Le equazioni $(1)$ e $(2)$ permettono di ricavare l’orbita successiva alla fionda gravitazionale.
