Abbiamo visto alcune caratteristiche delle onde gravitazionali nel breviario pubblicato qualche articolo fa. Qui proponiamo un’indagine semplificata della rilevazione delle onde gravitazionali presso LIGO o Virgo. Il rilevatore delle onde gravitazionali è un interferometro, come mostrato in figura:
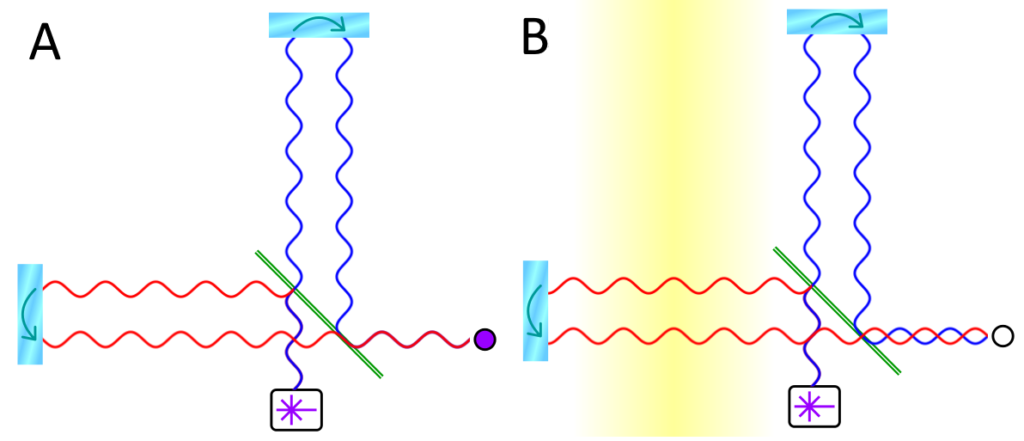
L’interferometro è composto da due bracci perpendicolari con due specchi in fondo; un laser (la scatolina) e una lente (la linea obliqua). La lente lascia passare metà del raggio laser verso l’alto, e ne riflette metà verso sinistra. I due raggi così separati raggiungono ognuno uno specchio, e sono riflessi indietro. La stessa lente li ricongiunge e li fa arrivare insieme su un punto (il pallino). Senza onda gravitazionale i due bracci hanno lunghezza identica: all’arrivo i due raggi laser sono in fase, quindi si rafforzano a vicenda e il pallino s’illumina.
Se invece passa un’onda gravitazionale (parte B) un braccio si allunga e l’altro si accorcia, come abbiamo visto nel breviario. Quando i due raggi laser si ricongiungono non sono più in fase, perché hanno percorso lunghezze diverse. Non essendo più in fase, si indeboliscono a vicenda e la luce sul pallino si affievolisce: in base a quanta luce arriva sul sensore possiamo ricostruire l’onda gravitazionale.
Avevamo visto che nel calibro trasverso a traccia nulla (TT) la metrica di un’onda gravitazionale che si propaga lungo l’asse $z$ prende la forma:
$$ds^2 = -dt^2 +[1+h(t)]dx^2+[1-h(t)]dy^2+dz^2$$
Questa è una delle due polarizzazioni possibili, che scegliamo per semplicità. Concentriamoci inoltre su uno solo dei bracci dell’interferometro, che supponiamo sia collocato lungo l’asse $x$. La metrica può essere quindi ulteriormente semplificata:
$$ds^2 = -dt^2 +[1+h(t)]dx^2$$
L’interferometro misura la differenza nei cammini luminosi, pertanto ci interessa il moto di un fotone ($ds^2=0$):
$$\left(\frac{dx}{dt}\right)^2 = \frac{c^2}{1+h(t)}$$
Nel calibro TT le coordinate degli oggetti non cambiano al passaggio dell’onda gravitazionale, mentre cambia però la distanza propria tra gli oggetti. Se immaginiamo le coordinate come una griglia, al passaggio dell’onda gli oggetti rimangono al loro posto sulla griglia, che però viene deformata, cambiando la distanza tra di essi. Pertanto il braccio del rilevatore lungo l’asse $x$ è sempre fisso tra i punti $x=0$ e $x=l$, e ciò che cambia è il tempo impiegato dalla luce a compiere il viaggio. È possibile utilizzare altre coordinate in cui la descrizione è diversa, ma il risultato finale è comunque lo stesso. L’intervallo di tempo infinitesimale soddisfa:
$$dt = \frac{\sqrt{1+h(t(x))}}{c}dx \approx \left(1+\frac{1}{2}h(t(x))\right) \frac{dx}{c}\tag{1}$$
dove abbiamo usato il fatto che $h$ è molto piccolo (tipicamente $\sim 10^{-21}$). Non conosciamo $t(x)$, ma possiamo approssimarlo. Al prim’ordine, $(1)$ diventa:
$$dt = \frac{dx}{c}$$
Per cui se $t$ è il tempo alla fine del percorso d’andata del fotone, $t(x)$ è il tempo quando il fotone si trova al punto $x$ e $L$ è il punto d’arrivo finale, integrando abbiamo:
$$t-t(x)=\frac{L-x}{c}\implies t(x)=t-\frac{L-x}{c}$$
Per cui risostituendo in $(1)$ abbiamo al prim’ordine in $h$:
$$dt = \left[1+\frac{1}{2}h\left(t-\frac{L-x}{c}\right)\right] \frac{dx}{c}$$
Integrando tra il punto di partenza e il punto di arrivo,
$$T_a(t) = \frac{L}{c} +\frac{1}{2c}\int_0^L h\left(t-\frac{L-x}{c}\right)dx$$
dove $T_a(t)$ ammette la seguente interpretazione: se il fotone finisce il viaggio d’andata al tempo $t$, allora ha impiegato un tempo $T_a(t)$ per compiere il viaggio d’andata.
Possiamo svolgere lo stesso ragionamento per il viaggio di ritorno del fotone, e otteniamo:
$$T_r(t) = \frac{L}{c} +\frac{1}{2c}\int_0^L h\left(t-\frac{x}{c}\right)dx$$
L’interpretazione è la stessa di sopra: se un fotone arriva alla fine del viaggio di ritorno al tempo $t$, allora avrà impiegato $T_r(t)$ per compiere il viaggio di ritorno. Pertanto mettendo insieme i due tempi abbiamo che il tempo totale è dato da:
$$T_{tot}(t) = T_a(t-T_r(t))+T_r(t) \approx T_a(t-L/c)+T_r(t)$$
L’espressione in $T_a$ è dovuta al fatto che il tempo $t$ è quello alla fine del viaggio, che coincide con la fine del viaggio del ritorno. Pertanto il fotone avrà terminato il viaggio di andata al tempo $t-T_r$.
Mettendo tutto insieme, otteniamo per la variazione lungo uno dei bracci:
$$T_{tot}(t)=2\frac{L}{c}+\frac{1}{2c}\int_0^L \left[h\left(t+\frac{x}{c}-\frac{2L}{c}\right)+ h\left(t-\frac{x}{c}\right)\right]dx$$
L’espressione può essere semplificata. Separando i due addendi dell’integrale e facendo alcuni cambi di variabile otteniamo:
$$T_{tot}(t)=2\frac{L}{c}+\frac{1}{2}\int_{t-2L/c}^{t}h(v)dv$$
Nel caso in cui $h$ vari lentamente col tempo (per onde di frequenze molto basse) possiamo portarlo fuori dall’integrale, e otteniamo il solito risultato per la variazione temporale:
$$\frac{T_{tot}(t)}{2L/c} -1 \approx \frac{1}{2}h(t)$$
Ora chiamiamo $L_x$ e $L_y$ le lunghezza dei due bracci dell’interferometro. Il calcolo per il braccio $y$ è lo stesso di quello per il braccio $x$, con l’eccezione che la metrica è diversa: bisogna sostituire $-h$ ad $h$. Per cui:
$$T_{tot,y}(t)=\frac{L_y}{2c}-\frac{1}{2}\int_{t-2L_y/c}^{t}h(v)dv$$
La differenza nei tempi di arrivo lungo i due bracci è quindi:
$$\delta T (t) = \frac{L_x-L_y}{2c}+\frac{1}{2}\int_{t-2L_x/c}^{t}h(v)dv+\frac{1}{2}\int_{t-2L_y/c}^{t}h(v)dv$$
