Simulazione numerica della divisione di Cassini

La divisione di Cassini è la separazione più grande presente negli anelli di Saturno (in figura):

Divisione di Cassini. Da Wikimedia.

Si dice che la divisione sia dovuta alla risonanza orbitale tra gli elementi dell’anello nell’orbita e una delle lune più piccole di Saturno, Mimas. Infatti la posizione della divisione è tale che un elemento che orbiti a quella distanza abbia velocità angolare pari al doppio di quella di Mimas. In questo modo orbita dopo orbita le posizioni di Mimas e degli elementi si riallineano sempre, e in questo modo l’influsso gravitazionale di Mimas si accumula col tempo.

Per testare questa teoria simuliamo numericamente il comportamento degli anelli. Sull’impalcatura del problema dei tre corpi ristretto per Saturno e Mimas, risolviamo numericamente la traiettoria di ognuno degli anelli indipendentemente. Nello scegliere questa impostazione abbiamo fatto tre principali approssimazioni:

• Abbiamo supposto che l’orbita di Mimas sia circolare (in questo caso $e\approx 0,02$, quindi l’approssimazione è buona
• Abbiamo ignorato le interazioni tra gli elementi dell’anello, che possono essere significative
• Abbiamo ignorato le interazioni con le altre lune di Saturno, che possono essere significative

Utilizziamo la stessa terminologia dell’articolo indicato sopra. In particolare in questo caso

$$\mu = \frac{M_{Mimas}}{M_{Saturno}+M_{Mimas}}\approx 7 \cdot 10^{-8}$$

Nell’effettuare la simulazione questo valore di $\mu$ è troppo piccolo per portare a risultati apprezzabili in tempi computazionalmente fattibili (quantomeno per il mio computer). Per cui scegliamo invece $\mu = 0.0001$.

Nel ricavare le equazioni del moto abbiamo posto $R=1$, quindi misuriamo le distanze in termini della distanza Saturno – Mimas, che è di circa $190000\,\mathrm{km}$. Gi anelli si estendono da circa $80000$ a $170000\,\mathrm{km}$ quindi circa da $0,4$ a $0,9$. La divisione di Cassini si estende dai $117000$ ai $122000\,\mathrm{km}$, che corrisponde ad una larghezza di $0,02$.

Abbiamo anche posto $\omega = 1$, quindi misuriamo il tempo nell’unità $T=2\pi$ dove $T$ è il periodo orbitale di Mimas (circa 23 ore).

Rimangono solo da definire le condizioni al contorno per l’integrazione. Disponiamo gli oggetti in anelli attorno a Saturno in coordinate polari con $0 < \theta < 2\pi$ e $0,4 < r < 0,9$. La velocità angolare di un’oggetto alla distanza $d$ dal centro di Saturno è

$$\Omega_d \approx \sqrt{\frac{G(M_{Sat}+M_{Mim})}{d^3}} = \frac{1}{d^{3/2}}$$

nelle unità in cui $\omega = \sqrt{G(M_{Sat}+M_{Mim})/R^3} = R = 1$. Pertanto per un moto circolare le condizioni al contorno sono

$$\begin{cases}
x = r \cos{\theta}\\
y = r \sin{\theta}\end{cases}\implies \begin{cases}\dot x = -r \sin{\theta} \dot \theta = -\frac{\sin{\theta}}{\sqrt{r}}\\ \dot y = r \cos{\theta} \dot \theta = \frac{\cos{\theta}}{\sqrt{r}}\end{cases}$$

Il problema è formulato nel sistema di coordinate $S’$ corotante con Mimas, mentre le condizioni al contorno sono formulate nel sistema esterno. Dobbiamo quindi ruotare le condizioni al contorno.

Poiché $\omega = 1$, la trasformazione tra $S$ e $S’$ è data da $\mathbf r = R(t) \mathbf r’$, dove

$$R(t) = \begin{pmatrix} \cos{t} & -\sin{t} & 0 \\ \sin{t} & \cos{t} & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

Per cui la posizione iniziale non cambia, come ci aspettiamo: $\mathbf r (0) = \mathbf r'(0)$.

Derivando, otteniamo la regola di trasformazione per le velocità:

$$\frac{d\mathbf r’}{dt}(0) = \frac{d\mathbf r}{dt}(0) + \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \mathbf r$$

A questo punto possiamo impostare la simulazione con $50000$ elementi. Partendo dagli anelli al tempo zero:

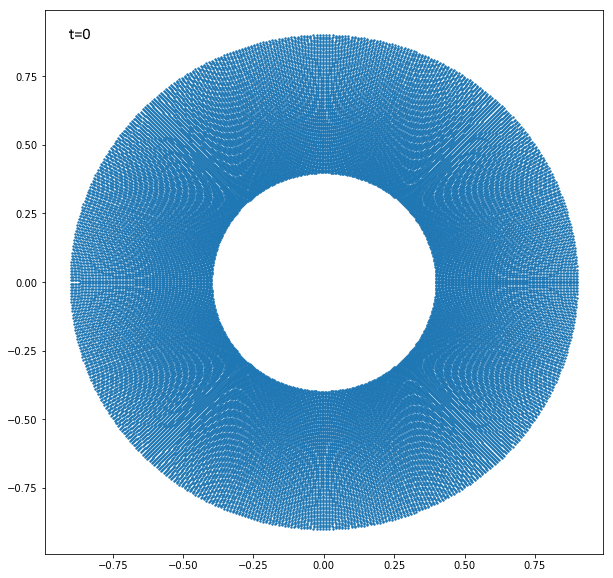
Anelli al tempo iniziale. Produzione mia usando Python.

Otteniamo al tempo $t = 200$, ovvero dopo circa $60$ orbite:

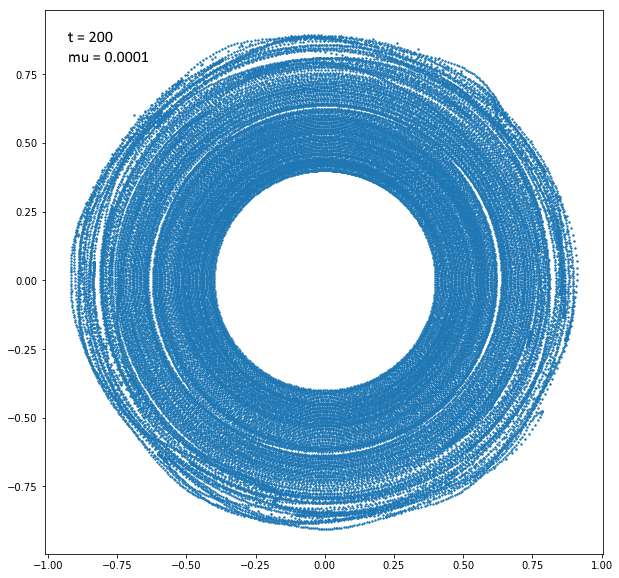
Anelli di Saturno influenzati da Mimas. Produzione mia usando Python.

Osserviamo che si è aperta una fenditura circa dove ci si aspetterebbe, che è la nostra divisione di Cassini. Tuttavia la fenditura non è abbastanza larga e ciò sembra essere confermato da ulteriori simulazioni: ci devono essere altri meccanismi in gioco.

Si è inoltre aperta un’altra divisione a $d \approx 0,74$, che corrisponde ad una risonanza $3 : 2$ con Mimas. Gli anelli esterni sembrerebbero destabilizzati, ma l’instabilità non sembra crescere in ulteriori simulazioni. È possibile che gli anelli esterni siano protetti da una risonanza con altre lune di Saturno.