Abbiamo già ricavato le cosiddette equazioni di Tolman-Oppenheimer-Volkoff e abbiamo mostrato come da esse si può ricavare un limite alla massa del nucleo di una stella fredda. Il problema che ci poniamo adesso è di estendere questo limite alla massa dell’intera stella. Possiamo farlo numericamente: partendo dalla massa e dal raggio del nucleo e integrando le equazioni TOV verso l’esterno della stella otteniamo la massa totale.
Per fare ciò dobbiamo supporre un’equazione di stato del gas, e pertanto dobbiamo sapere da cosa è formato. Ci occupiamo del caso di una stella a neutroni. A densità elevate, superiori a $\rho_N = 5 \cdot 10^{17} \mathrm{kg/m^3}$ non abbiamo idea di quale possa essere l’equazione di stato dei neutroni. La zona centrale in cui $\rho > \rho_N$ è il nucleo della stella a neutroni, per il quale abbiamo ottenuto la massa limite nell’articolo precedente. Partendo dal nucleo, integriamo numericamente nell’inviluppo, cioè la regione in cui $\rho < \rho_N$, e dobbiamo conoscerne l’equazione di stato.
Secondo la fisica statistica un gas di fermioni non relativistico a bassa densità ha l’equazione di stato della forma:
$$p(\rho)=\frac{3^{2/3}\pi^{4/3}}{5}\frac{\hbar^2}{m_n^{8/3}} \rho^{5/3}$$
dove $m_n$ è la massa del neutrone. In generale un’equazione della forma $p = K \rho^\gamma$ è detta politropica.
Ponendo $c=G=1$ possiamo esprimere tutti i valori in termini di $\mathrm{km}$, per cui
$$\rho_N = 5 \cdot 10^{17} \mathrm{kg/m^3}\approx 0,0003711\, \mathrm{km}^{-2}\\
K = \frac{3^{2/3}\pi^{4/3}}{5}\frac{\hbar^2}{m_n^{8/3}} \approx 288,6\, \mathrm{km}^{4/3}\\
m_{N\mathrm{max}} = \frac{4}{\sqrt{243 \pi \rho_N}} \approx 7,52\,\mathrm{km}\\
r_{N\mathrm{max}}=\frac{1}{\sqrt{3\pi \rho_N}} \approx 16,9\,\mathrm{km}$$
Le equazioni TOV diventano due equazioni in due incognite ($m,\rho$):
$$m’ = 4\pi r^2 \rho\\
\rho’ = -\frac{(K\rho +\rho^{2-\gamma})(m\rho^{1-\gamma}+4\pi r^3 K \rho)}{K\gamma r(r-2m)}$$
e le derivate sono prese rispetto al raggio $r$. L’integrazione inizia dal raggio $r_N$ del nucleo centrale con il valore $m_N$ della massa centrale. Calcoliamo la soluzione numerica dell’equazione TOV per tutti i valori iniziali di $r_N$ ed $m_N$ che rispettino le disuguaglianze:
$$m_N< \frac{2}{9} r_N \left[1-6\pi r_N^2 p(r_N) + \sqrt{1+6\pi r_N^2 p(r_N)}\right]\\
m_N > \frac{4}{3}\pi r_N^3 \rho_N$$
ovvero per tutti i valori permessi della massa del nucleo e della densità. Impostiamo l’integratore numerico per fermarsi quando $\rho=0$, cioè quando la stella è finita.
L’area d’integrazione è rappresentata nel grafico seguente:
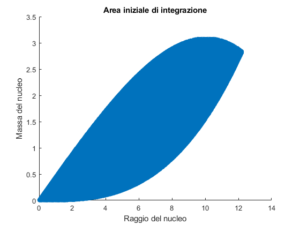
Un esempio tipico dell’andamento della massa e del raggio all’aumentare del raggio è mostrato nelle due figure seguenti:
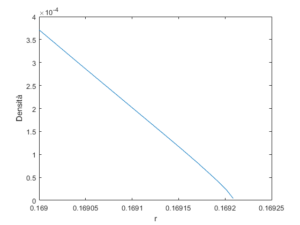
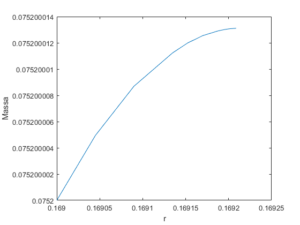
Il risultato della simulazione numerica in cui l’equazione per la stella è stata risolta per circa $130\mathrm{k}$ condizioni iniziali è invece mostrato nelle figure seguenti:
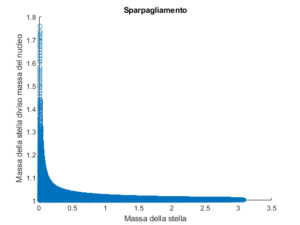
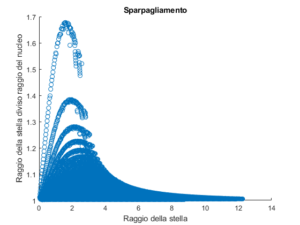
Come potete notare dal grafico, l’area d’integrazione è determinata dalle disuguaglianze sopraindicate, che dipendono da $p_N$ e quindi dall’equazione di stato e da $\rho_N$. Pertanto in questo caso il valore massimo che otteniamo per la massa ($\approx 3,1\,\mathrm{km} \approx 2,1 M_\odot$) è minore del valore massimo previsto per il nucleo ($\approx 5 M_\odot$). Il calcolo va quindi ripetuto per diversi valori di $\rho_N$, il cui valore è scelto da noi in base al grado di fiducia che abbiamo nell’equazione di stato che utilizziamo. I risultati sono mostrati nei grafici successivi:
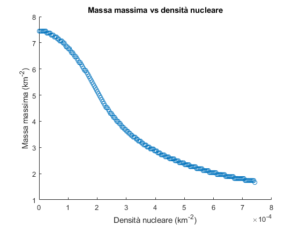
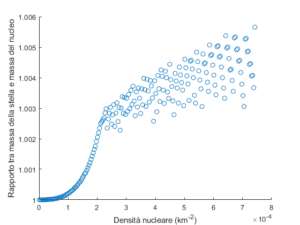
Variando la densità nucleare da $5\cdot 10^{15} \mathrm{kg/m^3}$ a $10^{18} \mathrm{kg/m^3}$ vediamo che per valori piccoli la massa massima della stella si avvicina alla massa massima del nucleo $7,52 \mathrm{km} \approx 5 M_\odot$. Come mostra la seconda immagine, l’inviluppo costituisce sempre meno dell’$1\%$ della stella.
Ciò che mostra la presente simulazione è che l’inviluppo è irrilevante nella determinazione della massa limite di una stella a neutroni. Infatti, come mostrato nei grafici sopra, quando la massa del nucleo si avvicina ai suoi valori massimi, il nucleo costituisce più del $99\%$ della massa della stella. Quindi il limite alla massa del nucleo $5M_\odot$ è anche la massa limite di una stella a neutroni: una stella più pesante di così è necessariamente un buco nero.
Ciò significa che nel tentativo di restringere ulteriormente il valore della massa limite di una stella a neutroni dobbiamo concentrarci sul trovare un valore limite alla massa del nucleo. Questo problema sarà affrontato nel prossimo articolo.