Nell’articolo precedente, abbiamo ricavato le equazioni del moto di un corpo che si muove nel campo gravitazionale prodotto da altri due più massicci:
$$\begin{cases}
\ddot x -2\omega \dot y= -\pdv{\Omega}{x}\\
\ddot y + 2\omega \dot x =-\pdv{\Omega}{y}
\end{cases}$$
dove
$$\Omega(x,y)=-\frac{GM_1}{\sqrt{(x-R_1)^2+y^2}}-\frac{GM_2}{\sqrt{(x-R_2)^2+y^2}}-\frac{1}{2}(x^2+y^2) $$
Per occuparci numericamente del problema è conveniente semplificare tutti i parametri. Poniamo quindi:
$$\omega = R = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mu = \frac{M_2}{M_1+M_2}$$
In questo modo le masse si trovano in $(\mu, 0)$ e $(\mu-1, 0)$ rispettivamente, e le equazioni diventano:
$$\boxed{\begin{cases}
\ddot x -2 \dot y= -\pdv{\Omega}{x}\\
\ddot y + 2 \dot x =-\pdv{\Omega}{y}
\end{cases}}$$
con
$$\Omega(x,y)=-\frac{(1-\mu)}{\sqrt{(x-\mu)^2+y^2}}-\frac{\mu}{\sqrt{(x+1-\mu)^2+y^2}}-\frac{1}{2}(x^2+y^2) $$
Di particolare interesse è la possibilità di orbite stazionarie, ovvero di particolari punti nei quali possiamo posizionare degli oggetti che nel sistema rotante rimangano fermi. Questi punti sono detti punti di Lagrange. Matematicamente si ottengono ponendo tutte le velocità a $0$, quindi:
$$\begin{cases}
\pdv{\Omega}{x}=0\\
\pdv{\Omega}{y}=0
\end{cases}$$
Ovvero sono i punti stazionari della funzione $\Omega$. È pertanto utile disegnarne un profilo altimetrico:
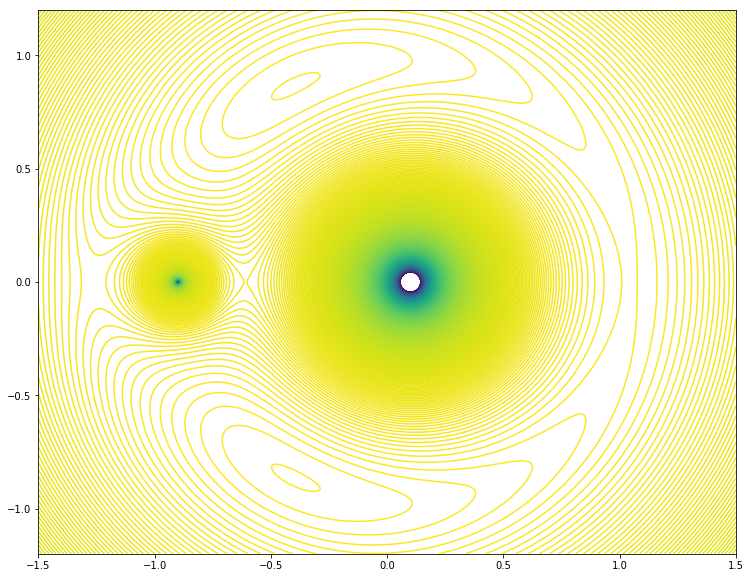
Profilo altimetrico di $\Omega$ per $\mu=0.1$
Per cui notiamo cinque punti stazionari: tre selle lungo la linea $y=0$ e due massimi/minimi sopra e sotto simmetricamente. Dove si trovano esattamente i punti stazionari? Esplicitando le equazioni che li determinano, troviamo che tre punti sono sulla linea $y=0$, ma le coordinate della $x$ sono date dalla soluzione di una quintica, che in generale è impossibile. Vedremo come calcolarne la posizione in un altro articolo. Nel caso dei due massimi/minimi sopra e sotto, possiamo invece risolvere l’equazione esattamente:
$$x=\mu-\frac{1}{2}\,\,\,\,\,\,y=\pm\frac{\sqrt{3}}{2}$$
ovvero formano un triangolo equilatero con le due masse principali. I tre punti lungo $y=0$ sono chiamati $L1$, $L2$ e $L3$, mentre gli altri due sono chiamati $L4$ e $L5$.
Stabilità dei punti di Lagrange
Analizziamo la stabilità dei punti di Lagrange. A tale scopo dobbiamo linearizzare le equazioni del moto. Poniamo infatti $x = x_0 + \epsilon$ e $y=y_0 +\eta$ e scompattiamo le due equazioni del second’ordine in quattro del prim’ordine. Per cui otteniamo in forma matriciale:
$$\frac{d}{dt}\begin{pmatrix} \epsilon \\ \eta \\ \dot \epsilon \\ \dot \eta \end{pmatrix} = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\\ -\Omega_{xx}(x_0,y_0) & -\Omega_{xy}(x_0,y_0) & 0 & 2 \\ -\Omega_{xy}(x_0,y_0) & -\Omega_{yy}(x_0,y_0) & -2 & 0\end{pmatrix} \begin{pmatrix} \epsilon \\ \eta \\ \dot \epsilon \\ \dot \eta\end{pmatrix}$$
dove la matrice è l’Hessiana del sistema. Ponendo $a = \Omega_{xx}(x_0,y_0)$, $b = \Omega_{xy}(x_0,y_0)$ e $c= \Omega_{yy}(x_0,y_0)$ otteniamo per gli autovalori dell’hessiana:
$$\lambda = \pm \frac{1}{\sqrt{2}} \sqrt{\pm\sqrt{(a+c+4)^2 -4(ac-b^2)}-(a+c+4)}$$
I tre punti collineari sono delle selle, per cui il determinante dell’Hessiana è negativo, $ac-b^2<0$. Per cui la quantità all’interno della radice interna è positiva, e prendendo tutti i segni positivi anche la quantità all’interno della radice esterna è positiva. In questo modo l’Hessiana ha un’autovalore positivo, per cui il sistema è instabile.
Per i due punti $L4$ e $L5$, poiché ne conosciamo esattamente la posizione, possiamo calcolare i valori della derivata seconda di $\Omega$:
$$a = -\frac{3}{4}\,\,\,\,\,\,\,\,\,\, b =-\frac{3\sqrt{3}}{2}\left(\mu-\frac{1}{2}\right)\,\,\,\,\,\,\,\,\,\, c = -\frac{9}{4}$$
Per cui gli autovalori sono:
$$\lambda = \pm \frac{1}{\sqrt{2}} \sqrt{\pm\sqrt{27\mu^2-27\mu+1}-1}$$
Le radici del polinomio all’interno della radice sono $\mu_\pm = \frac{1}{2}\pm \frac{1}{6}\sqrt{\frac{23}{3}}$. Per cui:
- Se $0<\mu < \mu_-$ oppure $\mu_+<\mu < 1$ allora il polinomio è compreso tra $0$ e $+1$, per cui la radice interna è reale e compresa tra $0$ e $+1$. Quindi la radice esterna ha argomento negativo: tutti gli autovalori del sistema sono immaginari e il sistema è stabile.
- Se $\mu_-<\mu < \mu_+$ allora il polinomio è negativo, per cui la radice interna darà un numero immaginario e l’argomento della radice esterna è un numero complesso con parte reale non nulla. Poiché c’è il più o meno davanti, uno degli autovalori avrà parte reale positiva, e il sistema è instabile.
Pertanto riassumendo, i tre punti $L1$, $L2$, $L3$ sono punti stazionari instabili: una piccola perturbazione porta un oggetto in uno dei tre punti ad allontanarsi da essi, per cui un eventuale missione spaziale in uno di questi punti avrà bisogno di propulsione per correggere l’orbita.
I due punti $L4$ ed $L5$ sono invece stabili, purché $\mu < 0,039$. I sistema Terra-Luna, Terra-Sole e Giove-Sole, ad esempio, soddisfano tutti questa condizione. In questo caso una piccola perturbazione dell’orbita induce un moto un po’ a caso attorno al punto di Lagrange. Minore è la perturbazione, minore è l’orbita indotta, che comunque rimane vincolata attorno al punto. Questa situazione è particolarmente visibile nel caso di Giove: i suoi punti $L4$ ed $L5$ sono infatti occupati da molteplici asteroidi detti “troiani”.
