Derivare le onde gravitazionali è una faccenda lunga e tediosa. Questo è un riassunto della teoria, per vedere i fatti principali senza rimanere azzoppati dai conti.
Sperimentalmente non osserviamo onde gravitazionali se non con difficoltà, per cui ne deduciamo che sono molto deboli e quindi per descriverle linearizziamo le equazioni della relatività generale. Partendo dall’equazione di Einstein:
$$R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu} = 8\pi T_{\mu\nu}\tag{*}$$
la linearizzazione della teoria si ottiene supponendo che la metrica si possa scrivere come:
$$g_{\mu\nu} = \eta_{\mu\nu}+h_{\mu\nu}$$
dove la perturbazione $h_{\mu\nu}$ è piccola, ovvero $| h_{\mu\nu}| \ll 1$. In pratica nell’effettuare i calcoli ignoriamo tutti i termini del second’ordine in $h_{\mu\nu}$ e in particolare alziamo e abbassiamo gli indici usando la metrica di Minkowski.
Il membro sinistro dell’equazione di Einstein può essere calcolato brutalmente: dalla metrica otteniamo i simboli di Christoffel, e quindi i tensori di curvatura. Il risultato è complicato, ma può essere semplificato. Per prima cosa lo scriviamo in termini della cosiddetta perturbazione a traccia rovesciata:
$$\bar{h}_{\mu\nu} = h_{\mu\nu}-\frac{1}{2}\eta_{\mu\nu}h^\rho_{\,\,\rho}$$
Inoltre la relatività generale è invariante rispetto ai diffeomorfismi, ma l’invarianza permane anche nella teoria linearizzata solo se è preservata al contempo la forma linearizzata della metrica. Possiamo utilizzare questa libertà residua per imporre la condizione $\partial^\nu \bar{h}_{\mu\nu}=0$. In questo modo l’equazione di Einstein $(*)$ prende una forma particolarmente semplice:
$$\partial^\rho \partial_\rho \bar{h}_{\mu\nu}=-16\pi T_{\mu\nu}$$
che è un’equazione d’onda relativistica col tensore energia-impulso come sorgente.
Nel caso del vuoto non ci sono sorgenti, quindi $T_{\mu\nu}=0$ e otteniamo la semplice equazione d’onda relativistica, la cui soluzione è data dalla sovrapposizione di onde piane:
$$\bar{h}_{\mu\nu} = H_{\mu\nu}e^{i k_\rho x^\rho}$$
Sostituendo nell’equazione d’onda otteniamo $k_\nu k^\nu=0$, cioè il vettore d’onda è nullo, ovvero l’onda viaggia alla velocità della luce. La condizione dell’invarianza per diffeomorfismi invece impone che $k^\nu H_{\mu\nu}=0$, ovvero l’onda gravitazionale è trasversale. Possiamo effettuare una nuova trasformazione applicando un diffeomorfismo in modo tale da imporre due ulteriori condizioni sull’ampiezza d’onda: $H_{0\mu}=0$ e $H^\mu_{\,\,\mu}=0$. Per un’onda che viaggia lungo l’asse $z$, queste condizioni si traducono nella seguente forma per l’ampiezza d’onda:
$$H_{\mu\nu}=\begin{pmatrix}0 & 0 & 0 & 0 \\ 0 & H_+ & H_\times & 0\\0 & H_\times & – H_+ & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$$
Le due costanti caratterizzano l’ampiezza dell’onda e corrispondono alle due possibili polarizzazioni di un’onda gravitazionale. Disponendo una serie di oggetti in cerchio nel vuoto, in modo che non ci siano forze tra essi, un’onda gravitazionale di passaggio perpendicolarmente al piano del cerchio lo fa oscillare verso un’ellisse nelle due direzioni. L’onda $H_+$ corrisponde al moto a sinistra, mentre la polarizzazione $H_\times$ è quella a destra:
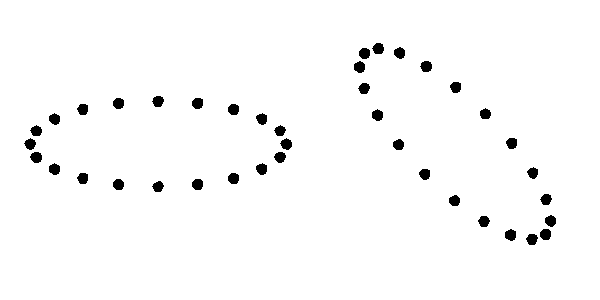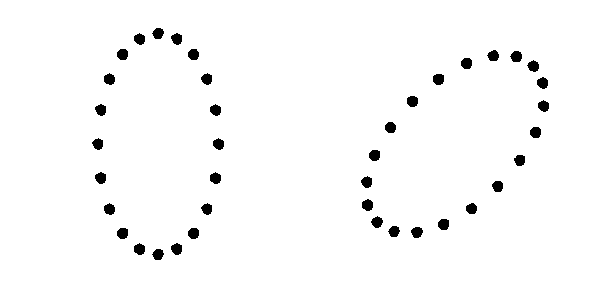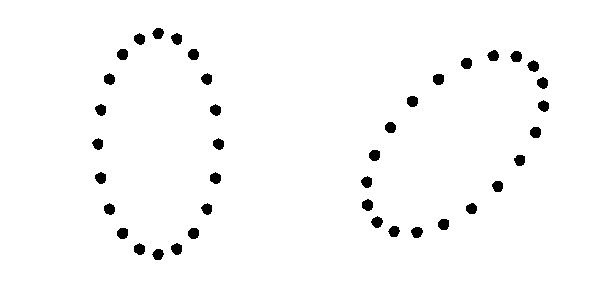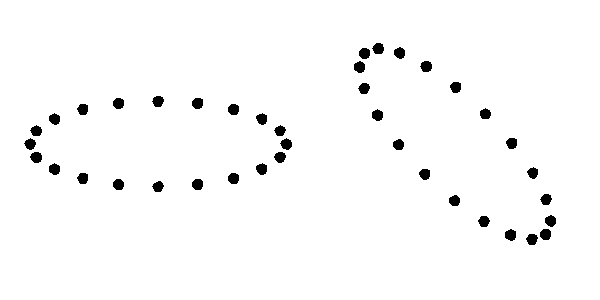
Effetto del passaggio di un’onda gravitazionale su degli oggetti disposti in cerchio nel vuoto
Nel caso in cui le onde sono generate da una sorgente, si tratta di risolvere l’equazione di Einstein linearizzata con $T_{\mu\nu}\neq 0$. La soluzione dell’equazione è gia stata trattata in un post precedente. Otteniamo:
$$\bar{h}_{\mu\nu}(t, \mathbf x) =4 \int d^3 \,\mathbf y \frac{T_{\mu\nu}(t-|\mathbf x -\mathbf y|, \mathbf y)}{|\mathbf x -\mathbf y|}$$
Il risultato è analogo a quello dei potenziali ritardati in elettromagnetismo.
Possiamo semplificare l’espressione supponendo che la dimensione della sorgente delle onde sia piccola rispetto alla distanza a cui vengono misurate. Sotto queste condizioni, ponendo $r=|\mathbf x|$ otteniamo:
$$\bar{h}_{\mu\nu}(t, \mathbf x) =\frac{4}{r} \int d^3 \,\mathbf y \,T_{\mu\nu}(t-r, \mathbf y)$$
Possiamo ottenere una formula semplificata per le componenti spaziali integrando per parti. Il termine di bordo sparisce poiché la sorgente è localizzata, per cui utilizzando la conservazione del tensore energia-impulso $\partial^\mu T_{\mu\nu}=0$ otteniamo
$$\bar{h}_{ij}(t, \mathbf x) = \frac{4}{r} \ddot{I}_{ij}(t-r)\,\,\,\,\,\,\,\mathrm{dove}\,\,\,\,\,\,\, I_{ij}(t-r) = \int d^3 \,\mathbf y\, T_{00}(t-r, \mathbf y) y^i y^j\,\,\,\,\,\,\,$$
Il tensore cartesiano $I_{ij}$ è detto secondo momento della densità di energia. L’espressione per $\bar{h}_{ij}$ è quella di un’onda sferica che si propaga verso fuori. Dalla formula vediamo che le onde gravitazionali sono prodotte da una sorgente che varia nel tempo; se la sorgente è periodica, le onde avranno la medesima periodicità.
A partire da questa formula, è possibile ricavare la cosiddetta formula del quadrupolo. Se definiamo il quadrupolo come il tensore $Q_{ij}=I_{ij}-(I_{kk}/3)\delta_{ij}$, ovvero la parte a traccia nulla del secondo momento della densità di energia, allora l’energia radiata dal sistema è data da:
$$\frac{dE}{dt}= -\frac{G}{5 c^5} \langle \dddot{Q}_{ij} \dddot{Q}_{ij}\rangle$$
La derivazione della formula è particolarmente ostica perché è impossibile definire una densità di energia locale per il campo gravitazionale (di qui la presenza della media, per cui l’energia è non-locale). Da quest’ultima formula otteniamo il risultato che una configurazione sfericamente simmetrica, quindi con $Q_{ij}=0$, non irradia onde gravitazionali. Per questo ricerchiamo onde provenienti soprattutto da sorgenti asimmetriche, come i sistemi binari.
Seguiamo Peters (1964) e Peters & Matthews (1963) nel considerare la radiazione dovuta ad un sistema newtoniano dei due corpi. In tal caso la densità di energia $T_{00}$ è data da due delta di Dirac centrate ognuna nella posizione delle due masse. Per cui $I_{ij} = m_1 (x_1)_i (x_1)_j + m_2 (x_2)_i (x_2)_j$ dove $x_1$ e $x_2$ sono la posizione delle due masse. Svolgendo i calcoli otteniamo
$$\frac{dE}{dt} = -\frac{32 G^4 (m_1 m_2)^2 (m_1+m_2)}{5 c^5 a^5} \left[\frac{1+\frac{73}{24}e^2+\frac{37}{96}e^4}{(1-e^2)^{7/2}}\right]$$
dove $a$ è il semiasse maggiore dell’orbita mentre $e$ è l’eccentricità. La perdita di energia aumenta notevolmente con l’eccentricità, e mostra un asintoto per $e\to 1$. Nel caso opposto, $e=0$, sappiamo dalla teoria newtoniana che $E=-G m_1 m_2/2a$. Sostituendo e risolvendo l’equazione differenziale, otteniamo l’equazione per il raggio:
$$a(t) = \left[a_0^4 -\frac{256 G^3 m_1 m_2 (m_1+m_2) }{5c^5}t\right]^{1/4}$$
ovvero il sistema tenderà alla collisione in tempo finito. Il caso generale (con $e \neq 0$ e variabile) può essere risolto numericamente utilizzando anche l’equazione per la perdita di momento angolare. In questo caso tanto l’eccentricità quanto il semiasse maggiore saranno progressivamente ridotti dall’emissione di onde gravitazionali.
