L’algebra di Clifford in due dimensioni
Nell’articolo precedente, abbiamo trovato l’algebra di Clifford su $\mathbb{R}^3$. Per denotare quest’algebra si usa per convenzione il simbolo $\mathcal{G}(\mathbb{R}^3)$. Per dare altri esempi di algebre di Clifford possiamo costruire $\mathcal{G}(\mathbb{R}^2)$ cioè l’algebra di Clifford su $\mathbb{R}^2$. La base standard di $\mathbb{R}^2$ è $\{e_1, e_2\}$. L’algebra ha dimensione $2^2=4$, e una base dell’algebra è data da:
$$\{1, \,\,e_1, e_2, \,\, e_1 e_2\}$$
La base è formata da un elemento di grado $0$, due elementi di grado $1$ e un elemento di grado $2$. Lo pseudoscalare di quest’algebra è $I = e_1 e_2$. Usando le regole del prodotto geometrico, possiamo calcolare
$$I^2 = e_1 e_2 e_1 e_2 = -e_1 e_1 e_2 e_2 = -(e_1)^2 (e_2)^2=-1$$
Grazie a questa proprietà, gli elementi in $\mathcal{G}(\mathbb{R}^2)$ della forma $a 1+b I$ si comportano come i numeri complessi. Cioè $\mathcal{G}(\mathbb{R}^2)$ include una copia di $\mathbb{C}$ data dal sottoinsieme generato da $\{1, I\}$. Poiché il sottoinsieme è chiuso rispetto al prodotto geometrico, esso forma una sottoalgebra isomorfa a $\mathbb{C}$.
Gli altri elementi sono quelli di grado 1, cioè i vettori, della forma:
$$x=a e_1 + b e_2$$
ovvero i soliti vettori in $\mathbb{R}^2$. Questi non formano un’algebra, perché il prodotto $e_1 e_2$ è fuori dall’insieme. Abbiamo un isomorfismo tra i vettori e gli elementi di grado pari, poiché:
$$e_1 x = a (e_1)^2 + b e_1 e_2 = a + b I$$
e viceversa se $z = a + b I $, allora:
$$e_1 z = a e_1 + b e_1 I = a e_1 + b e_2$$
Il ruolo privilegiato del vettore $e_1$ è chiaro: rappresenta l’asse reale. Dato $z\in \mathbb{C}$, possiamo scriverlo come $z = r e^{I \phi}$, e la rotazione del vettore è facilissima; basta moltiplicare per una fase:
$$z’ = e^{I \theta} z$$
Grazie all’isomorfismo che abbiamo trovato, otteniamo un’espressione per la rotazione di un vettore in $\mathbb{R}^2$:
$$x’ = e_1 z’ = e_1 e^{I \theta} z = e_1 e^{I \theta} e_1 x$$
L’esponenziale $e^{I \theta}$ è definito come serie di potenze. Inoltre
$$I e_1 = e_1 e_2 e_1 = -e_1 e_1 e_2 = -e_1 I$$
quindi lo pseudoscalare anticommuta con i vettori. Pertanto
$$e_1 e^{I \theta} e_1 = e_1 (\cos{\theta} + \sin{\theta} I ) e_1 =\cos{\theta} -\sin{\theta} I =e^{-I \theta}$$
e quindi:
$$x’ = e^{-I \theta} x = x e^{I \theta}=e^{-I \theta/2} x e^{I \theta/2}$$
è la formula della rotazione in due dimensioni di un vettore usando l’algebra di Clifford. L’ultima forma può sembrare strana, ma è quella più facile da generalizzare.
Chiamiamo $\mathcal{G}^+$ la sottoalgebra degli elementi di grado pari. L’esempio sopra ci dice che $\mathcal{G}^+(\mathbb{R}^2)=\mathbb{C}$ e illustra un fatto generale: gli elementi di grado pari formano un’algebra, perché il prodotto di due elementi di grado pari ha grado pari. Ciò non è vero per gli elementi di grado dispari, che quindi non formano un’algebra.
I quaternioni emergono naturalmente in 3D
Ora ritorniamo all’algebra $\mathcal{G}(\mathbb{R}^3)$, la cui base è:
$$\{1, \,\,e_1, e_2, e_3, \,\,e_1 e_2, e_2 e_3, e_1 e_3,\,\, e_1 e_2 e_3\}$$
Sappiamo già che $I^2=-1$. E gli elementi di grado 2? Troviamo che
$$(e_1 e_2)^2 = (e_2 e_3)^2 = (e_1 e_3)^2 = -1$$
Scalari e pseudoscalari formano di nuovo una sottoalgebra isomorfa a $\mathbb{C}$. La sottoalgebra $\mathcal{G}^+(\mathbb{R}^3)$ ha base:
$$\{1, \,\,e_1 e_2, e_2 e_3, e_1 e_3\}$$
Chiamando $i=e_1 e_2, j = e_2 e_3, k = e_1 e_3$, abbiamo le relazioni
$$i^2=j^2=k^2=ijk=-1$$
che è l’algebra dei quaternioni. Gli elementi di grado pari dell’algebra di Clifford dello spazio formano un’algebra isomorfa ai quaternioni, $\mathcal{G}^+(\mathbb{R}^3)\cong\mathbb{H}$.
Come ottenere il prodotto vettoriale
Inoltre, come promesso, possiamo scrivere il prodotto vettoriale in termini del prodotto esterno. In particolare:
$$a \times b = -I a \wedge b$$
Lo possiamo illustrare con un calcolo. Usando la notazione di Einstein, possiamo scrivere i due vettori come $a = a_i e_i$ e $b = b_i e_i$. Allora
$$a \wedge b = (a_i e_i) \wedge (b_j e_j) = a_i b_j e_i \wedge e_j = a_i b_j e_i e_j$$
Ora, $I e_1 e_2 = -e_3$, $I e_1 e_3 = e_2$, ecc. In generale, $I e_i e_j = -\epsilon_{ijk} e_k$, e quindi
$$I a \wedge b = -\epsilon_{ijk} a_i b_j = -(a \times b)_k$$
L’effetto della moltiplicazione per lo pseudoscalare è quello di trasformare un bivettore in un vettore. Questo è un esempio della trasformazione duale che tramite lo pseudoscalare mappa multivettori di grado $k$ in multivettori di grado $n-k$.
Proprietà dello pseudoscalare
Lo pseudoscalare $I$ è un elemento importante dell’algebra. Ha alcune proprietà importanti, che dipendono dalla dimensione $n$ dello spazio dell’algebra:
- se $n$ è dispari, lo pseudoscalare commuta con tutti gli elementi dell’algebra
- se $n$ è pari, lo pseudoscalare commuta con tutti e soli gli elementi di grado pari (questa è una differenza di cui tener conto se si vuole interpretarlo come $i\in \mathbb{C}$)
- Il quadrato dello pseudoscalare è dato da $I^2 = (-1)^{n(n-1)/2}s$, dove $s$ è il segno del determinante della metrica ($=1$ per spazi euclidei, $=-1$ per spazi lorentziani). Questo è un fatto puramente combinatorio.
Possiamo adoperare quest’ultima proprietà per definire una trasformazione duale, che mappa multivettori di grado $k$ in multivettori di grado $n-k$, data da:
$$x^c = x I^{-1}$$
Questa è una trasformazione simile (ma non uguale) al duale di Hodge delle forme differenziali. In particolare, usando le proprietà sopra, possiamo usarla per definire il prodotto vettoriale dal prodotto cuneo:
$$a \times b = (a \wedge b)^c$$
Le matrici di Pauli rappresentano l’algebra di Clifford in 3D
Se scriviamo il prodotto geometrico di due vettori base in $\R^3$, abbiamo la formula:
$$e_i e_j = e_i \cdot e_j + e_i \wedge e_j = \delta_{ij}+I \epsilon_{ijk} e_k$$
che è esattamente la formula per il prodotto delle matrici di Pauli. Infatti le matrici di Pauli formano una rappresentazione di un sottoinsieme dell’algebra di Clifford.
Rotazioni in tre dimensioni
Nella prima parte dell’articolo abbiamo visto come effettuare rotazioni in due dimensioni. Le algebre di Clifford ci forniscono un punto di vista innovativo su ciò che significa ruotare un oggetto. Nel caso bidimensionale abbiamo visto che la rotazione è implementata da un oggetto della forma $e^{\theta e_1 e_2}$, dove $e_1 e_2$ è il piano di rotazione. Ovvero, ciò che specifichiamo non è un angolo e un asse, bensì un angolo e un piano. Sembra un’innovazione banale, perché in tre dimensioni ad ogni piano corrisponde un asse (la sua normale) e viceversa. Ciò non è vero in un numero maggiore di dimensioni: ad ogni piano bidimensionale corrispondono più normali, e non ha più senso parlare di rotazione attorno ad un asse, ma solo di rotazione in un piano. La figura sotto da un’idea di cosa significa ruotare in un piano in tre dimensioni.
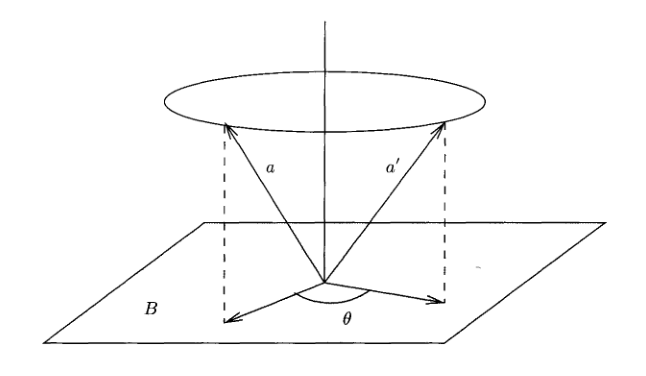
Il vettore a è ruotato di theta nel piano definito dal bivettore B. L’immagine è presa dal libro Geometric Algebra for Physicists (p.46).
Data la forma della rotazione di un vettore in $2D$, tiriamo ad indovinare quella in $3D$. Una rotazione nel piano $x-z$ potrebbe essere della forma:
$$x \to R x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R= e^{\theta e_1 e_3}$$
e facendo i conti scopriamo il risultato non è neanche un vettore. Allora ricordiamo che in $2D$ abbiamo scritto la rotazione anche in un altro modo:
$$x \to R^\dagger x R\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R= e^{\theta e_1 e_3/2}$$
dove $R^\dagger$ è il rovesciamento di $R$, ovvero ne rovescia l’ordine dei prodotti geometrici: ad esempio $(e_1 e_2 \cdots e_k)^\dagger = e_k \cdots e_2 e_1$. L’oggetto $R$ è detto rotore. In questo caso svolgendo i calcoli:
$$R = \cos{\left(\frac{\theta}{2}\right)}+e_1 e_3\sin{\left(\frac{\theta}{2}\right)}$$
$$x’ = R^\dagger x R = (x \cos{\theta}-z\sin{\theta}, y, z \cos{\theta}+x\sin{\theta})$$
che è la formula corretta. In generale, un piano è rappresentato da un bivettore unitario non nullo. Per cui la formula generale della rotazione è
Teorema. (Rotazione nell’algebra di Clifford) Dato un qualsiasi elemento $x \in \mathcal{G}$ la sua rotazione di un angolo $\theta$ sul piano $a \wedge b$ è data da
$$x \to R^\dagger x R \,\,\,\,\,\,\,\,\,\,\,\,R=e^{a \wedge b\,\theta/2}$$
Dimostrazione (euristica). Poiché $a \wedge b$ è un bivettore, $(a \wedge b)^\dagger = b \wedge a = -a \wedge b$ per cui $R^\dagger = R^{-1}$ e quindi $R R^\dagger = 1$. Per cui spiaccicare un vettore tra i due $R$ è un’operazione che ne preserva il prodotto interno, quindi è una trasformazione ortogonale. Inoltre ha determinante positivo perché è un’esponenziale (oppure perché è il prodotto di elementi di grado pari), quindi è una rotazione. Per convincerci che sia davvero una rotazione sul piano $a \wedge b$ possiamo considerare un vettore $c$ ortogonale al piano: questo anticommuta con $a$ e con $b$, quindi commuta con $a \wedge b$. Possiamo quindi commutarlo con $R$ e otteniamo che la rotazione non ha effetto su di esso, come ci aspettiamo. Ciò dimostra la formula nel caso dei vettori.
Per estenderla ai multivettori basta notare che ogni multivettore è un prodotto geometrico di vettori, quindi ad esempio per $x = abc$ prodotto di vettori,
$$x’ = R^\dagger x R = R^\dagger abc R = R^\dagger a R R^\dagger b R R^\dagger c R = a’ b’ c’$$
Pertanto la formula è valida per ogni elemento dell’algebra di Clifford. $\square$
Nel prossimo articolo vedremo alcune algebre di Clifford su metriche non euclidee.
