Le equazioni di Maxwell sono notoriamente asimmetriche. Ad esempio,
$\nabla \cdot {\textbf E} = \rho$
$\nabla \cdot {\textbf B} = 0$
A destra della prima equazione abbiamo la carica elettrica, mentre a destra della seconda c’è sempre $0$. L’interpretazione di questa asimmetria è che non esistono “cariche magnetiche”. Una calamita ha sempre due poli, e se la spezzate, anche i due pezzi avranno sempre due poli ognuno.
Che succede se ipotizziamo l’esistenza di una particella con “carica magnetica” $g$? Dovremmo aggiungere un termine di carica a destra della seconda equazione, e integrando otterremmo l’equivalente magnetico della forza di Coulomb:
$$F = \frac{g}{4 \pi r^2}$$
Quali sono le conseguenze quantistiche di un monopolo magnetico? Mettiamoci in presenza di un potenziale magnetico ${\textbf A}$ e facciamo muovere una particella con carica elettrica $q$ lungo un cammino chiuso $C$. Dall’effetto Aharonov-Bohm la funzione d’onda della particella acquisisce una fase:
$$\psi \to e^{i \alpha q /\hbar} \psi \,\,\,\,\,\,\,\,\,\, \alpha = \int_C {\textbf A} \cdot \textbf{dx}$$
Ora se abbiamo un monopolo magnetico, diciamo all’origine, $\nabla \cdot {\textbf B} \neq 0$, e quindi non è detto che ${\textbf A}$ esista. Poco male; possiamo usare il teorema di Stokes per scrivere
$$\alpha = \int_C {\textbf A} \cdot \textbf{dx}=\int_S {\textbf B} \cdot \textbf{dS}$$
Ora, mentre $C$ è ben definito, $S$ è una qualsiasi superficie racchiusa da $C$. Se prendessimo una qualsiasi superficie chiusa con al centro il monopolo sappiamo che
$$\int_{\textrm{superficie chiusa}} {\textbf B} \cdot {\textbf dS}=g$$
Essendo tale superficie chiusa non c’è un cammino che la racchiude. Quindi consideriamo due superfici, $S_1$ e $S_2$ rappresentate in figura; la prima è quella ovvia “dentro” $C$, l’altra è quella “fuori” $C$ che racchiude il monopolo, tale che $S_1 + S_2$ sia una superficie chiusa con dentro il monopolo.
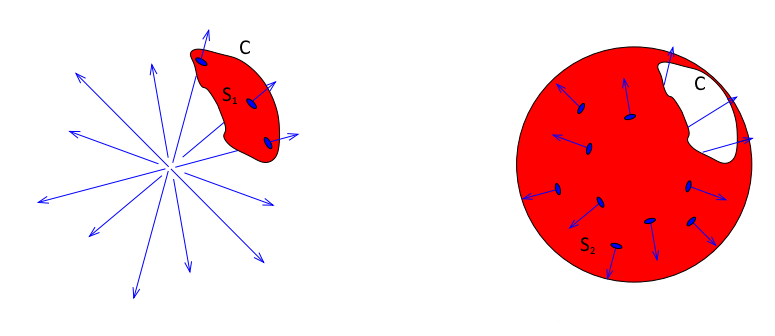
Le due superfici di integrazione. Presa dagli appunti di David Tong.
Le due superfici hanno orientazione opposta perché vedono il percorso $C$, che ha una direzione, “da lati diversi”. Quindi in particolare:
$$\int_{S_1} {\textbf B} \cdot {\textbf dS} -\int_{S_2} {\textbf B} \cdot {\textbf dS}= \int_{\textrm{superficie chiusa}} {\textbf B} \cdot {\textbf dS}=g$$
dove il segno meno è dovuto all’orientazione opposta. Ovvero se, come abbiamo visto all’inizio, $\alpha_1$ e $\alpha_2$ sono le fasi acquisite dalla funzione d’onda lungo il cammino $C$, calcolate in due modi diversi, allora abbiamo
$$\alpha_1 -\alpha_2 = g$$
ovvero nonostante il cammino sia lo stesso, la fase acquisita dalla funzione d’onda dipende da come la calcoliamo. Normalmente la fase della funzione d’onda è irrilevante perché si cancella. Ma se ad esempio invece di misurare $\psi$ misuriamo $\phi+\psi$, dove $\phi$ non cambia, allora la probabilità $\abs{\phi + e^{iq\alpha/\hbar} \psi}^2$ dipende anche dalla fase $\alpha$.
Perciò, nonostante $\alpha_1$ e $\alpha_2$ siano diverse, devono dare lo stesso risultato fisico, quindi devono soddisfare:
\begin{align*}
e^{i q \alpha_1 /\hbar}=e^{i q \alpha_2 /\hbar}\\
\implies \frac{q}{\hbar} (\alpha_1-\alpha_2) = 2 n \pi\\
\implies q g = 2\pi \hbar n\\
\end{align*}
Quest’ultima è la condizione che cercavamo, detta condizione di Dirac. Interpretando superficialmente, la condizione afferma che se esiste anche solo un monopolo magnetico nell’universo, allora la carica elettrica è quantizzata.
In termini più moderni, abbiamo due possibilità: o tutte le cariche elettriche sono multipli interi di una carica minima, e quindi possiamo avere monopoli magnetici; oppure esistono due cariche elettriche il cui rapporto è un numero irrazionale, e la condizione sopra proibisce i monopoli magnetici.
Le due possibilità corrispondono alla scelta di un gruppo di gauge/calibro per l’elettromagnetismo ($U(1)$ oppure $\mathbb{R}$, rispettivamente). Poiché i fisici sono convinti che la prima sia la scelta corretta, credono anche che i monopoli magnetici possano esistere.
