I raggi di luce provenienti da un’astronave relativistica sono concentrati “verso avanti”. Questo fenomeno è noto come “effetto fanale” o anche “aberrazione relativistica”. In questo articolo deriviamo l’effetto e lo visualizzeremo.
Un astronave si muove con velocità $v$ lungo la direzione $x$ del sistema $S$, e un fanale sull’astronave emette un fotone con quadrimpulso $P’$ nel sistema a riposo dell’astronave, che chiamiamo $S’$.
Poiché il quadrimpulso è un quadrivettore, soggetto ad una trasformazione di Lorentz da $S$ a $S’$ esso trasforma secondo la legge:
$$P’=\Lambda P$$
dove
$$\Lambda = \begin{pmatrix}
\gamma & -\gamma v/c & 0 & 0\\
-\gamma v/c & \gamma & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}$$
Consideriamo ora un fotone che si muove nel piano $xy$ in $S$ con un angolo $\theta$ rispetto all’asse $x$. Il quadrimpulso del fotone è:
$$P = \begin{pmatrix} E/c \\ p\sin\theta \\ p\cos\theta \\ 0 \end{pmatrix}$$
Pertanto applicando la trasformazione di Lorentz:
$$\begin{pmatrix} E’/c \\ p’\sin\theta’ \\ p’\cos\theta’ \\ 0 \end{pmatrix}= \begin{pmatrix}
\gamma & -\gamma v/c & 0 & 0\\
-\gamma v/c & \gamma & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix} \begin{pmatrix} E/c \\ p\sin\theta \\ p\cos\theta \\ 0 \end{pmatrix} $$
Da ciò otteniamo:
$$E’ = \gamma E (1-\beta \cos\theta)\\
p’ \cos\theta’ = \gamma E/c (\cos\theta -\beta)$$
dove come al solito $\beta = v/c$. Per un fotone $p’ = E’/c = \gamma E/c (1-\beta \cos\theta)$, quindi:
$$\cos\theta’ = \frac{\cos\theta -\beta}{1-\beta \cos\theta}$$
Ora supponiamo una sorgente puntiforme e isotropa di fotoni in $S’$, ovvero il fanale dell’astronave. Se il fotone è emesso con un angolo $\theta$ in $S’$, allora in $S$ si misura un angolo
$$\cos\theta = \frac{\cos\theta’+\beta}{1+\beta\cos\theta’}$$
questo perché se $S’$ si muove con velocità $v$ rispetto a $S$, allora $S$ si muoverà con velocità $-v$ rispetto a $S’$, quindi per ottenere le formule inverse basta mandare $\beta \to -\beta$.
L’effetto di questa relazione è quella di schiacciare verso avanti tutti i raggi emessi. La visualizzazione grafica è piuttosto chiara:
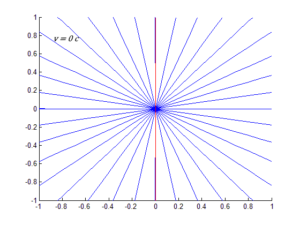
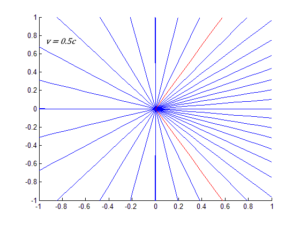
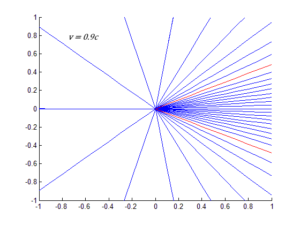
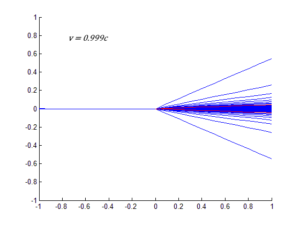
Quando $v$ si avvicina molto a $c$, tutti i fotoni sono diretti verso avanti nel sistema a riposo, tranne per il fotone sparato in direzione esattamente opposta al moto. Un oggetto che si muove a velocità relativistiche sarà quindi di difficile osservazione a meno che non ci si trova direttamente davanti all’oggetto stesso. L’effetto fanale ha implicazioni in astronomia.
